 por Flavio50 » Seg Abr 27, 2015 14:03
por Flavio50 » Seg Abr 27, 2015 14:03
1)Qual é a Equação da reta tangente á curva da equação y= X^2 - 3x no ponto da abscissa x =4
2)Um objeto se move conforme a função s(T) = 2t +3t^2 , que nos da sua posição em função do tempo. ao calcular sua velocidade instantanea quando t = 2 segundos.
3 Um Engenheiro precisa calcular o coeficiente angular da reta tangente á curva Y = 7x^3 + 4 no ponto em que x = 0. qual o valor do coeficiente.
meus resultados não batem alguém pode me ajudar com essas questoes. obrigado!
-
Flavio50
- Novo Usuário

-
- Mensagens: 5
- Registrado em: Dom Abr 19, 2015 12:41
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Mecanica
- Andamento: cursando
 por adauto martins » Seg Abr 27, 2015 19:36
por adauto martins » Seg Abr 27, 2015 19:36
equaçao da reta:
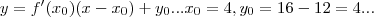
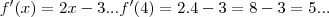
...
logo...

...
ps-cade os administradores e criadores do site pra limpar essa sujeira porno...
-
adauto martins
- Colaborador Voluntário

-
- Mensagens: 1171
- Registrado em: Sex Set 05, 2014 19:37
- Formação Escolar: EJA
- Área/Curso: matematica
- Andamento: cursando
 por Flavio50 » Ter Abr 28, 2015 09:38
por Flavio50 » Ter Abr 28, 2015 09:38
A resposta deu certinho vc pode me ajudar com as outras duas?
-
Flavio50
- Novo Usuário

-
- Mensagens: 5
- Registrado em: Dom Abr 19, 2015 12:41
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Mecanica
- Andamento: cursando
 por Cleyson007 » Ter Abr 28, 2015 15:36
por Cleyson007 » Ter Abr 28, 2015 15:36
Vou te ajudar com a questão n° 02)
A velocidade instantânea num tempo qualquer é dada pela derivada d(s)/d(t) = v (Derivada da posição em relação ao tempo)
s(T) = 2t +3t^2 (Função horária da posição)
Dado que d(s)/d(t) = v, temos:
v(t) = 2 + 6t
Para t=2, temos:
v(2) = 2 + 6(2) = 14m/s
Bons estudos
-

Cleyson007
- Colaborador Voluntário

-
- Mensagens: 1228
- Registrado em: Qua Abr 30, 2008 00:08
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática UFJF
- Andamento: formado
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Questoes complicadas
por tigre matematico » Sáb Out 15, 2011 09:02
- 2 Respostas
- 1773 Exibições
- Última mensagem por tigre matematico

Sáb Out 15, 2011 23:34
Polinômios
-
- questoes complicadas
por tigre matematico » Sáb Out 15, 2011 23:30
- 0 Respostas
- 807 Exibições
- Última mensagem por tigre matematico

Sáb Out 15, 2011 23:30
Números Complexos
-
- AJUDA QUESTOES, POR FAVOR, OBRIGADO
por aspirantestudante » Dom Jun 13, 2010 02:22
- 6 Respostas
- 6506 Exibições
- Última mensagem por karla_paula

Dom Jun 13, 2010 23:36
Funções
-
- Ajuda nessas questões de Trigonometria por favor!!
por g3brito » Seg Set 05, 2016 22:36
- 0 Respostas
- 2807 Exibições
- Última mensagem por g3brito

Seg Set 05, 2016 22:36
Trigonometria
-
- Ajuda com questões de derivadas! Urgente!
por arthurvct » Qua Jun 05, 2013 15:59
- 1 Respostas
- 1080 Exibições
- Última mensagem por ericaguedes_

Sáb Jun 08, 2013 00:07
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 3 visitantes
Assunto:
Exercicios de polinomios
Autor:
shaft - Qua Jun 30, 2010 17:30

Então, o exercicio pede para encontrar

.
Bom, tentei resolver a questão acima desenvolvendo as duas partes em ( )...Logo dps cheguei em um resultado q nao soube o q fazer mais.
Se vcs puderem ajudar !
Assunto:
Exercicios de polinomios
Autor:
Douglasm - Qua Jun 30, 2010 17:53
Bom, se desenvolvermos isso, encontramos:

Para que os polinômios sejam iguais, seus respectivos coeficientes devem ser iguais (ax = bx ; ax² = bx², etc.):


Somando a primeira e a segunda equação:

Finalmente:

Até a próxima.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


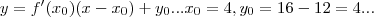
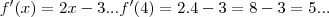 ...
... ...
...


 .
.



