por Roni Martins » Sáb Fev 13, 2010 15:30
Opa, boa tarde...estou com dificuldades em resolver esta questão de geometria envolvendo angulos...espero que voçes possam me ajudar..
tal questão pede para calcular a soma dos quatro angulos que estão na figura:
- Imagem 1 do exercicio
Sei que devo trabalhar com o suplemento dos angulos e com a definição de angulo externo...mas na hora de igualar uma equação na outra(pois vamos cair em varias equaçoes com varias variaveis), todas se anulam...
se voçes puderem me ajudar...
desde ja agradeço
obs: acho que devo começar o exercicio com na figura 2
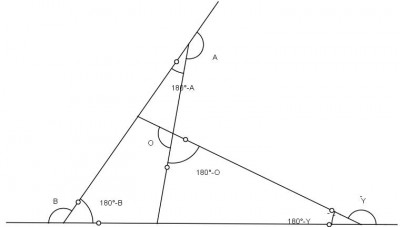
- figura 2
-
Roni Martins
- Novo Usuário
-
- Mensagens: 7
- Registrado em: Qui Fev 11, 2010 12:34
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: curso de graduação em matemática
- Andamento: cursando
por MarceloFantini » Dom Fev 14, 2010 00:32
Boa noite.
Fiz na figura, espero que entenda:
Espero ter ajudado.
Um abraço.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador
-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
por Roni Martins » Dom Fev 14, 2010 11:53
Oi, Bom dia Fantini, tudo bem?
Poxa, eu estava trabalhando com os angulos externos errados, depois da tua explicação atraves da imagem clareou tudo...
muito obrigado, tenha um otimo final de semana e um bom carnaval!
Abraços!
-
Roni Martins
- Novo Usuário
-
- Mensagens: 7
- Registrado em: Qui Fev 11, 2010 12:34
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: curso de graduação em matemática
- Andamento: cursando
Voltar para Geometria Plana
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Teorema de Tales
por LuanRodrigues » Qua Mai 04, 2011 23:42
- 1 Respostas
- 2589 Exibições
- Última mensagem por FilipeCaceres
Qua Mai 04, 2011 23:46
Geometria Plana
-
- Teorema de Tales
por LuanRodrigues » Qui Mai 05, 2011 21:26
- 1 Respostas
- 4970 Exibições
- Última mensagem por Molina
Sex Mai 06, 2011 12:52
Geometria Analítica
-
- teorema de tales
por bmachado » Seg Mar 26, 2012 17:51
- 3 Respostas
- 2515 Exibições
- Última mensagem por ednaldo1982
Sex Mar 30, 2012 01:11
Geometria Plana
-
- Teorema de Tales
por Jhenrique » Seg Nov 12, 2012 04:59
- 0 Respostas
- 1298 Exibições
- Última mensagem por Jhenrique
Seg Nov 12, 2012 04:59
Álgebra Elementar
-
- [Teorema de Tales]
por Giudav » Dom Nov 25, 2012 17:18
- 1 Respostas
- 2261 Exibições
- Última mensagem por e8group
Dom Nov 25, 2012 18:52
Geometria Plana
Usuários navegando neste fórum: Nenhum usuário registrado e 8 visitantes
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Thassya - Sáb Out 01, 2011 16:20
1) Para que os pontos (1,3) e (-3,1) pertençam ao grafico da função f(X)=ax + b ,o valor de b-a deve ser ?
2)Qual o maior valor assumido pela função f : [-7 ,10] em R definida por f(x) = x ao quadrado - 5x + 9?
3) A função f, do primeiro grau, é definida pos f(x)= 3x + k para que o gráfico de f corte o eixo das ordenadas no ponto de ordenada 5 é?
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Neperiano - Sáb Out 01, 2011 19:46
Ola
Qual as suas dúvidas?
O que você não está conseguindo fazer?
Nos mostre para podermos ajudar
Atenciosamente
Assunto:
[Função] do primeiro grau e quadratica
Autor:
joaofonseca - Sáb Out 01, 2011 20:15
1)Dados dois pontos A=(1,3) e B=(-3,1) de uma reta, é possivel definir a sua equação.
Em
substitui-se
m, substitui-se
y e
x por um dos pares ordenados, e resolve-se em ordem a
b.
2)Na equação
não existem zeros.Senão vejamos
Completando o quadrado,
As coordenadas do vertice da parabola são
O eixo de simetria é a reta
.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
f(-7)=93
f(10)=59
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
