Olá, estou com dúvida nesta questão:
Um professor dispõe de seis questões de Álgebra e quatro questões de Geometria para elaborar provas compostas por duas questões de Álgebra e duas de Geometria. O total de provas diferentes que esse professor pode elaborar é:
Tentei montá-la com 4 quadrinhos e dispondo as possibilidades em cada quadrinho, mas não deu certo. Fica um número muito alto. Tentei também separar as questões de álgebra e de geometria e depois juntá-las, também sem sucesso.



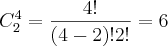
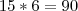 provas diferentes.
provas diferentes.


 .
.
 :
: