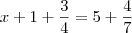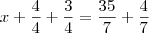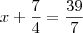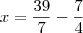por juniorthai » Qui Fev 11, 2010 15:19
que numero é necessário somar a um e tres quartos para se obter cinco e quatro setimos?
da uma força ai gente...obrigado
-
juniorthai
- Novo Usuário
-
- Mensagens: 4
- Registrado em: Seg Fev 08, 2010 12:00
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
por MarceloFantini » Qui Fev 11, 2010 15:55
Boa tarde.
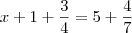
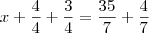
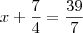
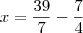
Basta resolver.
Espero ter ajudado.
Um abraço.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador
-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
Voltar para Sistemas de Equações
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Fração] Ajuda em problema de fração.
por smlspirit » Sex Mai 18, 2012 01:17
- 3 Respostas
- 3641 Exibições
- Última mensagem por DanielFerreira
Dom Mai 20, 2012 17:06
Álgebra Elementar
-
- problema com fração!
por leandro moraes » Ter Jan 19, 2010 18:37
- 5 Respostas
- 4685 Exibições
- Última mensagem por Elcioschin
Qui Jan 21, 2010 15:09
Estatística
-
- problema de fração
por hevhoram » Qua Jun 02, 2010 20:28
- 1 Respostas
- 2199 Exibições
- Última mensagem por MarceloFantini
Qui Jun 03, 2010 03:28
Álgebra Elementar
-
- Problema com fração
por junior_gyn » Dom Abr 24, 2011 15:52
- 2 Respostas
- 4295 Exibições
- Última mensagem por NMiguel
Dom Abr 24, 2011 16:31
Desafios Médios
-
- Problema com fração
por junior_gyn » Dom Abr 24, 2011 16:55
- 1 Respostas
- 2663 Exibições
- Última mensagem por NMiguel
Dom Abr 24, 2011 17:16
Desafios Médios
Usuários navegando neste fórum: Nenhum usuário registrado e 4 visitantes
Assunto:
Simplifique a expressão com radicais duplos
Autor:
Balanar - Seg Ago 09, 2010 04:01
Simplifique a expressão com radicais duplos abaixo:
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png "\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}")
Resposta:
Dica:
![\sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png "\sqrt[]{2}")
(dica : igualar a expressão a
e elevar ao quadrado os dois lados)
Assunto:
Simplifique a expressão com radicais duplos
Autor:
MarceloFantini - Qua Ago 11, 2010 05:46
É só fazer a dica.
Assunto:
Simplifique a expressão com radicais duplos
Autor:
Soprano - Sex Mar 04, 2016 09:49
Olá,
O resultado é igual a 1, certo?
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
