 por Padoan » Qui Fev 11, 2010 14:43
por Padoan » Qui Fev 11, 2010 14:43
Considere a função:
f (x) = x se x é racional, 1/x se x é irracional
Qual o maior elemento do conjunto?
{ f (7/31), f (1), f (3,14), f ( ? 24/? 2) }
Alguem saberia me explicar como se chega no resultado?
-
Padoan
- Novo Usuário

-
- Mensagens: 9
- Registrado em: Qui Fev 11, 2010 14:34
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por Molina » Qui Fev 11, 2010 15:00
por Molina » Qui Fev 11, 2010 15:00
Boa tarde.
Primeiramente você tem que identificar dessas alternativas que o problema sugere, quais são racionais e quais são irracionais.
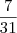
Racional

Racional
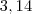
Racional.
Lembrando que \pi é irracional, mas 3,14 é racional. 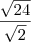
Irracional
Os racionais vamos considerar eles mesmos, pela função

e o irracional vamos considerar o inverso dele, pela função

. Seguindo a ordem...

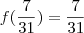
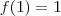
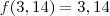
e

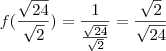
A dica está ai. Agora tente encontrar um jeito de verificar qual deles que é maior.

Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por Padoan » Qui Fev 11, 2010 15:07
por Padoan » Qui Fev 11, 2010 15:07
ah sim, eu estava contando o 3,14 como irracional... falta de atenção aqui.
Obrigado!
-
Padoan
- Novo Usuário

-
- Mensagens: 9
- Registrado em: Qui Fev 11, 2010 14:34
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por Molina » Qui Fev 11, 2010 15:20
por Molina » Qui Fev 11, 2010 15:20
Padoan escreveu:ah sim, eu estava contando o 3,14 como irracional... falta de atenção aqui.
Obrigado!
Tem que ver como tá descrito na questão. Se for só 3,14 eu consideraria racional, pois pode ser escrito como
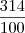
. Mas se tivesse 3,14... eu consideraria irracional, talvez por que o enunciado quer sugerir o

.

Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
Voltar para Funções
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- ajuda
por Daiane kelly » Seg Mar 24, 2008 22:38
- 4 Respostas
- 6377 Exibições
- Última mensagem por Cleyson007

Ter Mai 12, 2009 17:43
Matrizes e Determinantes
-
- Ajuda
por Umbus » Sáb Out 18, 2008 14:12
- 2 Respostas
- 3668 Exibições
- Última mensagem por lopes

Sáb Jun 20, 2009 15:51
Álgebra Linear
-
- Ajuda.
por VanessaFontela » Qui Dez 04, 2008 10:32
- 0 Respostas
- 2893 Exibições
- Última mensagem por VanessaFontela

Qui Dez 04, 2008 10:32
Matemática Financeira
-
- Ajuda!!!
por GABRIELA » Seg Set 21, 2009 17:28
- 1 Respostas
- 2283 Exibições
- Última mensagem por Molina

Seg Set 21, 2009 19:56
Sistemas de Equações
-
- Ajuda!!!!!!
por GABRIELA » Ter Set 22, 2009 16:35
- 6 Respostas
- 4411 Exibições
- Última mensagem por GABRIELA

Qui Set 24, 2009 16:29
Sistemas de Equações
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 12:41
pessoal eu achei como resultado 180 toneladas,entretanto sei que a questão está erra pela lógica e a resposta correta segundo o gabarito é 1.800 toneladas.
me explique onde eu estou pecando na questão. resolva explicando.
78 – ( CEFET – 1993 ) Os desabamentos, em sua maioria, são causados por grande acúmulo de lixo nas encostas dos morros. Se 10 pessoas retiram 135 toneladas de lixo em 9 dias, quantas toneladas serão retiradas por 40 pessoas em 30 dias ?
Assunto:
dúvida em uma questão em regra de 3!
Autor:
Douglasm - Qui Jul 01, 2010 13:16
Observe o raciocínio:
10 pessoas - 9 dias - 135 toneladas
1 pessoa - 9 dias - 13,5 toneladas
1 pessoa - 1 dia - 1,5 toneladas
40 pessoas - 1 dia - 60 toneladas
40 pessoas - 30 dias - 1800 toneladas
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:18
pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:21
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
valeu meu camarada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



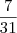 Racional
Racional Racional
Racional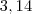 Racional. Lembrando que \pi é irracional, mas 3,14 é racional.
Racional. Lembrando que \pi é irracional, mas 3,14 é racional. 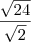 Irracional
Irracional e o irracional vamos considerar o inverso dele, pela função
e o irracional vamos considerar o inverso dele, pela função  . Seguindo a ordem...
. Seguindo a ordem...
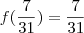
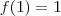
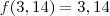

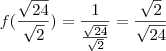



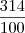 . Mas se tivesse 3,14... eu consideraria irracional, talvez por que o enunciado quer sugerir o
. Mas se tivesse 3,14... eu consideraria irracional, talvez por que o enunciado quer sugerir o  .
.
