Geometria simplissima

[GMAT2010]

Galera,

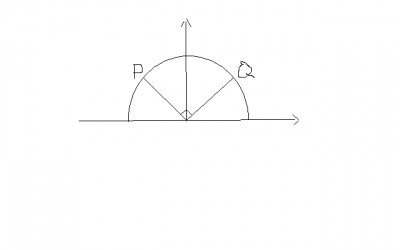
É uma questão que me parece muito fácil, porém não sei o que errei. Na figura em anexo, um semicírculo tem dois pontos, ponto P e ponto Q. Pela figura, as retas que ligam a origem do círculo a esse ponto tem o mesmo comprimento (raio) e o ângulo entre as duas retas é de 90 graus.
A pergunta é: se P = (- , 1), e Q = (s, t), qual o valor de "s"?

Para mim, parecia lógico que s = , porém a resposta diz que é s = 1.

Alguém entende o porque???

Ps: desculpem o desenho....

[Molina]

Alguém entende o porque???

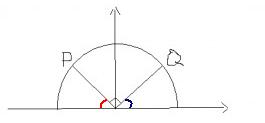
Olhando o desenho que eu refiz...

angulo.JPG (3.29 KiB) Exibido 856 vezes

... note que o enunciado não afirma em nada que os ângulos vermelho e azul são iguais. O fato de ter 90° entre as retas não nos garante isso.

O desenho que você fez até que dá impressão de que os ângulos que eu desenhei são iguais, mas imagina agora você girando o ângulo reto para a esquerda (mantendo os 90°). Com isso o ponto P chegaria mais próximo do eixo x e o ponto Q chegaria mais próximo do eixo y.

Espero ter ajudado a desvendar o porquê de nao ser .


Bom estudo,