 por hissamo » Sex Abr 10, 2015 15:57
por hissamo » Sex Abr 10, 2015 15:57
Sendo

e

as raízes da equação

, obtenha:
a)

=
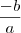
=

.
b)

=

=

.
c)
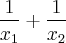
= Resposta e 7,por que?
obs:estou com dificuldades na letra C, pois nao consegui achar valor exato de x1 e x2 e resolvendo a equaçao 2° grau a raiz delta nao cai em um numero exato, se puderem me ajudar agradeço.
-
hissamo
- Novo Usuário

-
- Mensagens: 1
- Registrado em: Sex Abr 10, 2015 15:43
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por DanielFerreira » Sáb Abr 11, 2015 17:14
por DanielFerreira » Sáb Abr 11, 2015 17:14
Olá
Hissamo, seja bem-vindo(a)!
A partir das alíneas
a e
b podes chegar a resposta da
c. Repare que,
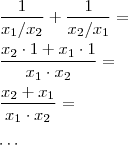
Resta-te substituir... Se tiveres dúvidas, retorne; se conseguires também!
"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação

-
- Mensagens: 1732
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Mangaratiba - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
Voltar para Equações
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [raízes de números complexos] Raízes de uma equação com grau
por karenfreitas » Seg Ago 22, 2016 19:08
- 1 Respostas
- 8111 Exibições
- Última mensagem por adauto martins

Sáb Ago 27, 2016 16:11
Números Complexos
-
- Raizes de equação de grau>=3
por spyderkill » Qua Mai 09, 2012 17:31
- 2 Respostas
- 2424 Exibições
- Última mensagem por pedroaugustox47

Sex Mai 11, 2012 02:33
Polinômios
-
- Raizes de equação de grau>=3
por citadp » Qua Jun 20, 2012 09:32
- 3 Respostas
- 2276 Exibições
- Última mensagem por Russman

Sex Jul 06, 2012 15:49
Cálculo: Limites, Derivadas e Integrais
-
- Raizes de uma equação de terceiro grau.
por 380625 » Dom Mar 27, 2011 13:58
- 3 Respostas
- 3009 Exibições
- Última mensagem por MarceloFantini

Dom Mar 27, 2011 18:09
Funções
-
- equação de segundo grau( descobrindo as raizes)
por arturmedeiros2010 » Qui Fev 13, 2014 15:34
- 1 Respostas
- 1353 Exibições
- Última mensagem por Russman

Sex Fev 14, 2014 00:15
Equações
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
cálculo de limites
Autor:
Hansegon - Seg Ago 25, 2008 11:29
Bom dia.
Preciso de ajuda na solução deste problema, pois só chego ao resultado de 0 sobre 0.
Obrigado
\lim_{x\rightarrow-1} x³ +1/x²-1[/tex]
Assunto:
cálculo de limites
Autor:
Molina - Seg Ago 25, 2008 13:25

Realmente se você jogar o -1 na equação dá 0 sobre 0.
Indeterminações deste tipo você pode resolver por L'Hôpital
que utiliza derivada.
Outro modo é transformar o numerador e/ou denominador
para que não continue dando indeterminado.
Dica: dividir o numerador e o denominador por algum valor é uma forma que normalmente dá certo.

Caso ainda não tenha dado uma

, avisa que eu resolvo.
Bom estudo!
Assunto:
cálculo de limites
Autor:
Guill - Dom Abr 08, 2012 16:03



Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 e
e  as raízes da equação
as raízes da equação  , obtenha:
, obtenha: =
= 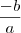 =
=  .
. =
=  =
=  .
.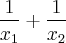 = Resposta e 7,por que?
= Resposta e 7,por que?




 , avisa que eu resolvo.
, avisa que eu resolvo.

