 por Miya » Dom Abr 05, 2015 13:06
por Miya » Dom Abr 05, 2015 13:06
olá! estou tentando resolver mas estou com dificuldades
Seja f a função de IR em IR definida por f(x)= x² - 3x+4 . Calcular:
a) - 1/3
b) ?¯3
c) 1-?¯2
a letra A eu fiz assim:
a)f(-1/3)=(-1/3)²-3(-1/3)+4
1/9+3/3+4
1+9+36/9= 46/9
b)f(?¯3)= (?¯3)²-3?¯3+4
a raíz corta com o número ² então fica 3-3?¯3+4
aí eu travo,com essa e a letra c também... poderiam me ajudar?
-
Miya
- Usuário Ativo

-
- Mensagens: 15
- Registrado em: Qui Mar 05, 2015 16:27
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por DanielFerreira » Dom Abr 05, 2015 14:06
por DanielFerreira » Dom Abr 05, 2015 14:06
Olá
Miya, boa tarde!
A letra "a" está incorreta.
a)

b)
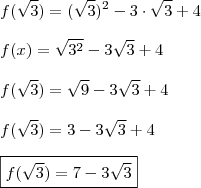
Miya, revise o assunto e tente resolver a "c", ok?!
"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação

-
- Mensagens: 1732
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Mangaratiba - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
 por Miya » Dom Abr 05, 2015 14:23
por Miya » Dom Abr 05, 2015 14:23
ah obrigada!
fica assim :
f(1-?¯2) = (1-?¯2)²-3(1-?¯2)+4
ai a raíz do dois corta com o dois elevado né,fica assim:
1-2-3(1-?¯2)+4
ai eu multiplico aquele 3 pelo parentesis né? fica assim:
1-2- 3-3?¯2+4
??
-
Miya
- Usuário Ativo

-
- Mensagens: 15
- Registrado em: Qui Mar 05, 2015 16:27
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por DanielFerreira » Sáb Abr 25, 2015 22:31
por DanielFerreira » Sáb Abr 25, 2015 22:31
Não. Lembre-se que
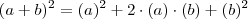
.
Portanto,

Tente concluir!
"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação

-
- Mensagens: 1732
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Mangaratiba - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
Voltar para Funções
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- funções(ajudem por favor!!)
por pauloleigo » Sex Set 16, 2011 03:36
- 1 Respostas
- 1360 Exibições
- Última mensagem por Neperiano

Sex Set 16, 2011 15:28
Funções
-
- Funções de lucro, por favor ajudem
por Deise_schmidt » Sex Abr 08, 2011 00:19
- 2 Respostas
- 3233 Exibições
- Última mensagem por Deise_schmidt

Sex Abr 08, 2011 14:03
Funções
-
- Me ajudem por favor.
por diegodalcol » Qui Mai 22, 2008 13:26
- 4 Respostas
- 4991 Exibições
- Última mensagem por admin

Qui Mai 22, 2008 16:33
Funções
-
- Por favor, ajudem-me!
por hindu » Qua Set 23, 2009 23:08
- 4 Respostas
- 4761 Exibições
- Última mensagem por Lucas Avilez

Ter Out 06, 2009 20:36
Cálculo: Limites, Derivadas e Integrais
-
- M ajudem por favor!!
por Biacbd » Seg Jan 18, 2010 15:39
- 0 Respostas
- 3460 Exibições
- Última mensagem por Biacbd

Seg Jan 18, 2010 15:39
Lógica
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 10:38
Olá ! Tenho essa dúvida e não consigo montar o problema para resolução:
Qual é o racional não nulo cujo o quadrado é igual à sua terça parte ?
Grata.
Assunto:
Conjunto dos números racionais.
Autor:
MarceloFantini - Sex Fev 18, 2011 12:27

Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 12:55
também pensei que fosse assim, mas a resposta é

.
Obrigada Fantini.
Assunto:
Conjunto dos números racionais.
Autor:
MarceloFantini - Sex Fev 18, 2011 13:01

Como

:

O que você fez?
Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 16:17
eu só consegui fazer a igualdade, não consegui desenvolver o restante, não pensei em fatoração, mas agora entendi o que vc fez.
Obrigada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



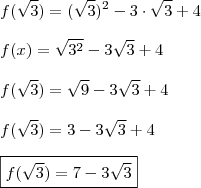

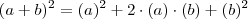 .
.

 .
.
 :
: