Considere os vetores
a: i + 3j + 2k
b: 2i - j + k
c: i - 2j
Seja 'pi' um plano paralelo aos vetores b e c e 'r' uma reta perpendicular ao plano 'pi'. Ache a projeção ortogonal do vetor a sobre a reta r.



 =
=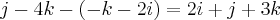 =v
=v ...
...

 ...calcule ai,o cosseno e tera o angulo de proj....
...calcule ai,o cosseno e tera o angulo de proj....

Larissa28 escreveu:Considere os vetores
a: i + 3j + 2k
b: 2i - j + k
c: i - 2j
Seja 'pi' um plano paralelo aos vetores b e c e 'r' uma reta perpendicular ao plano 'pi'. Ache a projeção ortogonal do vetor a sobre a reta r.
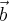 e
e 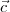 são paralelos ao plano
são paralelos ao plano  , calculando o vetor ortogonal aos dois através do produto vetorial, temos que o vetor normal será perpendicular ao plano. Ora, se o vetor normal é perpendicular ao plano e a reta
, calculando o vetor ortogonal aos dois através do produto vetorial, temos que o vetor normal será perpendicular ao plano. Ora, se o vetor normal é perpendicular ao plano e a reta  é perpendicular ao plano, podemos concluir que o vetor normal do plano é paralelo ao vetor diretor de
é perpendicular ao plano, podemos concluir que o vetor normal do plano é paralelo ao vetor diretor de  .
. :
: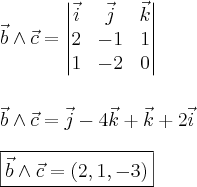
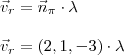
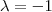 . Portanto,
. Portanto, 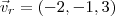 .
. sobre a reta
sobre a reta  .
.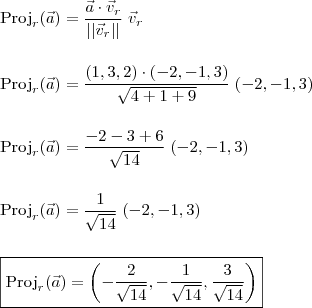


Voltar para Geometria Analítica
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png) (dica : igualar a expressão a
(dica : igualar a expressão a  e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)