Estou trabalhando em um modelo e para resolvê-lo preciso calcular a esperança de uma variável normal, condicional a outras duas normais. Mais especificamente:
Tenho três variáveis normais, independentes entre si:
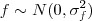
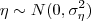
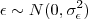
A variável
é a que interessa aos agentes do modelo, mas eles não a observam. A cada período, observam apenas dois sinais, a partir dos quais procuram extrair informações sobre :
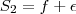
Em geral: trabalho com modelos em que tenho apenas um sinal (por exemplo,
), a partir do qual calculo a esperança condicional ![E[f|S_1=s_1]](/latexrender/pictures/a8aec9480e3251315705921d4b1555c7.png "E[f|S_1=s_1]")
considerando a distribuição conjunta, de modo que (sendo 
o coeficiente de correlação):![E[f|S_1=s_1] & = E[f] + \frac{Cov[f,s_1]}{Var[s_1]} (s_1-E[s_1]) = E[f] + \rho \frac{\sigma_f}{\sigma_{s_1}} (s_1-E[s_1])](/latexrender/pictures/417efc536f433f705c3331380055647c.png "E[f|S_1=s_1] & = E[f] + \frac{Cov[f,s_1]}{Var[s_1]} (s_1-E[s_1]) = E[f] + \rho \frac{\sigma_f}{\sigma_{s_1}} (s_1-E[s_1])")
Porém, dessa vez preciso de
![E[f|S_1=s_1, S_2=s_2]](/latexrender/pictures/e20b42eb3f8f02aea8ebe915e9063302.png "E[f|S_1=s_1, S_2=s_2]")
, a esperança condicional com três variáveis normais. Infelizmente, não estou conseguindo generalizar a fórmula para três ou mais variáveis. Alguém poderia me ajudar com isso, por favor?
Desde já, agradeço a atenção!
por 
, avisa que eu resolvo.
