 por killerkill » Seg Mar 16, 2015 17:24
por killerkill » Seg Mar 16, 2015 17:24
Pessoal, estou tentando entender a ideia intuitiva de um campo vetorial conservativo pro caso de integrais de linha. Meus conceitos estão muito embaralhados e gostaria da ajuda de alguém pra ajudar a organiza-los. Pelo que eu entendi até agora no meu curso, a integral de linha pode ser interpretada de varias formas, como uma área sobre uma curva até a função (espécie de cortina), como densidade em determinado ponto da curva e na parte onde estou tendo mais dificuldades, em um campo vetorial. Nessa ultima eu me embolo completamente quando se envolve o conceito de campo conservativo. Em uma curva fechada C1, imerso num campo conservativo, se selecionarmos um ponto "A" pertencente a essa curva e realizarmos uma volta completa na curva, a integral de linha (ou deveria eu dizer trabalho?) sobre essa curva é igual a zero. Ou seja, independe do caminho. Acho que não entendi o porquê. O único caso que consegui imaginar tentando fazer uma lógica foi o seguinte: imaginei uma curva em 3 dimenões imersa no campo gravitacional. Se eu partir de um ponto P1 na parte mais alta da curva(mais distante do centro do campo) e largar uma partícula imaginária, a força gravitacional irá atuar até que ela chegue ao ponto mais baixo da curva realizando um trabalho W1. Pro caso dessa partícula retornar ao ponto P1 o trabalho seria W2, de mesma intensidade que W1 porém agora contrária ao campo, ou seja, com valor negativo. Nesse caso, intuitivamente fica claro pensar que essa integral seria igual a zero. Essa ideia é correta?



 ,onde V um espaço vetorial sobre um corpo K...
,onde V um espaço vetorial sobre um corpo K...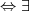 uma funçao
uma funçao 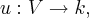 tal q.
tal q. 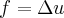 ,onde
,onde 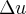 e o gradiente u em V...usando o teorema de stokes,mostra-se q. ...
e o gradiente u em V...usando o teorema de stokes,mostra-se q. ...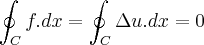 ,ou seja vai independer dos pontos inicias e finais,ou indepedente do caminho...
,ou seja vai independer dos pontos inicias e finais,ou indepedente do caminho...