De logo pode não parecer, mas este sistema é um sistema linear 2x2.
Obviamente, não é um sistema linear 2x2 nas variáveis x e y. É um sistema linear nas variáveis

e

tais que
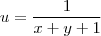

.
Note que fazendo essa
mudança de variáveis o sistema se transforma para
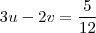
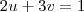
que é um sistema linear 2x2.
Corriqueiramente fazemos isso em Matemática. Solver um problema desconhecido consiste, basicamente, em transformá-lo em um problema o qual já sabemos a solução.
Facilmente, determinamos que a solução do sistema transformado é

. Daí, retornando a transformação,
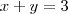
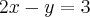
cuja solução é, facilmente,
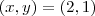
.





 e
e  tais que
tais que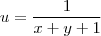
 .
.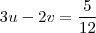
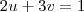
 . Daí, retornando a transformação,
. Daí, retornando a transformação, 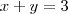
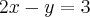
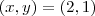 .
.

