 por Leonardo Ribeiro » Sáb Mar 07, 2015 01:28
por Leonardo Ribeiro » Sáb Mar 07, 2015 01:28
Fala pessoal, estou começando a estudar Equações Diferenciais agora. Já nos primeiros exercícios me deparei com uma coisa intrigante.
O enunciado é simples: Resolva a Equação Diferencial
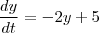
Acontece que fazendo por dois caminhos bem pouco diferentes, obtenho resultados diferentes por um sinal.
Método 1
Método 2 resumido
Agora o invés de multiplicar a equação por

, multiplico por

. Assim eu retiro o sinal negativo do


Mas como agora temos o "-2" e não "2" do lado direito da equação, desenvolvendo assim como no primeiro caminho iremos chegar em:
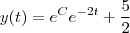
E o fato de o denominador mudar de
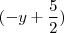
para
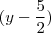
não influencia porque com o jogo de sinais que é feito no primeiro método utilizando a propriedade do ln, essa diferença desaparece.
A diferença na solução é só que em uma aparece o fator
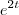
e na outra, o fator
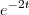
A resposta no gabarito é
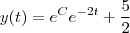
.
Eu poderia simplesmente continuar os exercícios e sempre que aparecer uma questão assim eu multiplicar a equação por um fator que tire o sinal negativo do

, até porque é assim que é ensinado nas resoluções do livro. Mas eu não iria conseguir dormir tranquilo haha.
Alguém mais experiente poderia explicar qual foi o erro que cometi para chegar em duas respostas diferentes? Sinto que deve ser algo muito simples, talvez até algum erro de sinal no meio do caminho.
Obs: Vão me desculpando se ficou confuso de entender. Tentei organizar ao máximo.
-
Leonardo Ribeiro
- Novo Usuário

-
- Mensagens: 4
- Registrado em: Sex Mar 06, 2015 23:57
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Mecânica
- Andamento: cursando
 por Russman » Sáb Mar 07, 2015 04:45
por Russman » Sáb Mar 07, 2015 04:45
O erro está na primeira solução. O seu erro foi substancial.
A função logaritmo é tal que leva produtos em somas. Isto é,
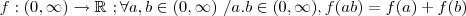
Daí, é possível mostrar que

. Mas

desde que

,

e
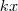
pertençam ao domínio de

, que é

.
Seu erro foi supor ln(kx) = k ln(x).
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
 por Leonardo Ribeiro » Sáb Mar 07, 2015 11:58
por Leonardo Ribeiro » Sáb Mar 07, 2015 11:58
Muito obrigado!
Quando resolvi ir pelo segundo caminho logo que chegou no ln eu fiz uma pesquisa no Google sobre as propriedades, que não me recordava. O problema é que já fui buscando por uma que me desse que kln(x) = ln(kx). O primeiro link que cliquei foi um do Yahoo respostas com um usuário citando a propriedade. Nem pensei duas vezes, tomei como verdade e utilizei hahah.
Era só ter feito um teste rápido e visto que é falso.
Obrigado mais uma vez!
-
Leonardo Ribeiro
- Novo Usuário

-
- Mensagens: 4
- Registrado em: Sex Mar 06, 2015 23:57
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Mecânica
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Equações Diferenciais] Exercício URGENTE!
por lucasfbfb » Seg Nov 17, 2014 10:36
- 2 Respostas
- 1470 Exibições
- Última mensagem por lucasfbfb

Seg Nov 17, 2014 15:23
Cálculo: Limites, Derivadas e Integrais
-
- Equações diferenciais
por tiagofabre » Sex Set 21, 2012 00:48
- 1 Respostas
- 1863 Exibições
- Última mensagem por MarceloFantini

Sex Set 21, 2012 01:14
Cálculo: Limites, Derivadas e Integrais
-
- equacoes diferenciais
por Thais Bomfim » Qua Dez 12, 2012 01:58
- 2 Respostas
- 2193 Exibições
- Última mensagem por Thais Bomfim

Qua Dez 12, 2012 14:02
Equações
-
- Equações Diferenciais
por sergio2205 » Qua Mar 06, 2013 13:27
- 1 Respostas
- 1737 Exibições
- Última mensagem por Russman

Qua Mar 06, 2013 15:14
Equações
-
- Equações Diferenciais
por marinalcd » Sex Ago 09, 2013 15:19
- 1 Respostas
- 1635 Exibições
- Última mensagem por Man Utd

Dom Jun 15, 2014 17:40
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 5 visitantes
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Thassya - Sáb Out 01, 2011 16:20
1) Para que os pontos (1,3) e (-3,1) pertençam ao grafico da função f(X)=ax + b ,o valor de b-a deve ser ?
2)Qual o maior valor assumido pela função f : [-7 ,10] em R definida por f(x) = x ao quadrado - 5x + 9?
3) A função f, do primeiro grau, é definida pos f(x)= 3x + k para que o gráfico de f corte o eixo das ordenadas no ponto de ordenada 5 é?
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Neperiano - Sáb Out 01, 2011 19:46
Ola
Qual as suas dúvidas?
O que você não está conseguindo fazer?
Nos mostre para podermos ajudar
Atenciosamente
Assunto:
[Função] do primeiro grau e quadratica
Autor:
joaofonseca - Sáb Out 01, 2011 20:15
1)Dados dois pontos A=(1,3) e B=(-3,1) de uma reta, é possivel definir a sua equação.


Em

substitui-se
m, substitui-se
y e
x por um dos pares ordenados, e resolve-se em ordem a
b.

2)Na equação

não existem zeros.Senão vejamos
Completando o quadrado,

As coordenadas do vertice da parabola são

O eixo de simetria é a reta

.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
f(-7)=93
f(10)=59
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
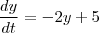

, multiplico por
. Assim eu retiro o sinal negativo do
para
não influencia porque com o jogo de sinais que é feito no primeiro método utilizando a propriedade do ln, essa diferença desaparece.
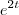 e na outra, o fator
e na outra, o fator 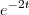
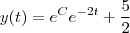 .
. , até porque é assim que é ensinado nas resoluções do livro. Mas eu não iria conseguir dormir tranquilo haha.
, até porque é assim que é ensinado nas resoluções do livro. Mas eu não iria conseguir dormir tranquilo haha. 
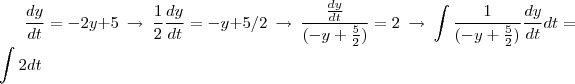

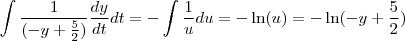

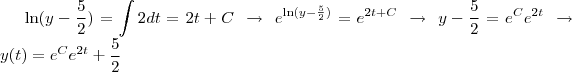


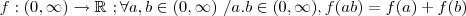
 . Mas
. Mas  desde que
desde que  ,
, e
e 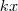 pertençam ao domínio de
pertençam ao domínio de  , que é
, que é  .
.


 substitui-se
substitui-se 
 não existem zeros.Senão vejamos
não existem zeros.Senão vejamos

 .Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.