 por ViniciusAlmeida » Seg Fev 09, 2015 12:35
por ViniciusAlmeida » Seg Fev 09, 2015 12:35
Bom dia! Comecei a estudar há alguns dias limites pelo livro do James Stewart e me deparei com esse exercício ainda na primeira parte do assunto:
Use um gráfico para estimar as equações de todas as assíntotas verticais da curva:
y = tan (2 sen(x)) com
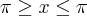
Fiz o gráfico usando o wolfram
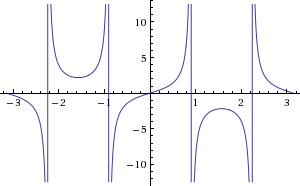
- WolframAlpha--y___tg__2_sen_x____x_from____to_____Plot__2015_02_10_1443.gif (5.06 KiB) Exibido 925 vezes
Consegui identificar assíntotas observando o gráfico em:
x

-0,9
x

0,9
x

2,2
x

-2,2
Porém, não consegui identificar uma fórmula geral. Como posso achar? Obrigado desde já!
GABARITO:
-
ViniciusAlmeida
- Usuário Ativo

-
- Mensagens: 24
- Registrado em: Seg Fev 09, 2015 12:13
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Grafico de limites e assintotas
por Bruhh » Qui Abr 15, 2010 15:43
- 3 Respostas
- 5295 Exibições
- Última mensagem por Marcampucio

Sex Abr 16, 2010 21:07
Cálculo: Limites, Derivadas e Integrais
-
- Encontrando assíntotas... gráfico
por Talitafreire » Qui Jul 09, 2009 17:29
- 2 Respostas
- 2600 Exibições
- Última mensagem por Talitafreire

Qui Jul 09, 2009 18:03
Cálculo: Limites, Derivadas e Integrais
-
- Limites(assíntotas)
por Luciano Dias » Dom Jan 03, 2010 12:37
- 3 Respostas
- 7573 Exibições
- Última mensagem por Molina

Dom Jan 03, 2010 23:22
Cálculo: Limites, Derivadas e Integrais
-
- Limites(assíntotas)correção
por Luciano Dias » Seg Jan 04, 2010 14:05
- 5 Respostas
- 5223 Exibições
- Última mensagem por Marcampucio

Qua Jan 06, 2010 20:16
Cálculo: Limites, Derivadas e Integrais
-
- LIMITES ( ASSINTOTAS VERTICAIS)
por belinha26 » Dom Set 29, 2013 17:16
- 1 Respostas
- 1558 Exibições
- Última mensagem por young_jedi

Dom Set 29, 2013 19:32
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 10 visitantes
Assunto:
função demanda
Autor:
ssousa3 - Dom Abr 03, 2011 20:55
alguém poderia me ajudar nesse exercício aqui Uma loja de CDs adquire cada unidade por R$20,00 e a revende por R$30,00. Nestas condições,
a quantidade mensal que consegue vender é 500 unidades. O proprietário estima que, reduzindo o preço para R$28,00, conseguirá vender 600 unidades por mês.
a) Obtenha a função demanda, supondo ser linear
Eu faço ensino médio mas compro apostilas de concursos para me preparar para mercado de trabalho e estudar sozinho não é fácil. Se alguém puder me ajudar aqui fico grato
Assunto:
função demanda
Autor:
ssousa3 - Seg Abr 04, 2011 14:30
Gente alguém por favor me ensine a calcular a fórmula da função demanda

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
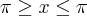
 -0,9
-0,9 0,9
0,9 2,2
2,2 -2,2
-2,2

