Problema de lógica envolvendo Seno

por **Guga1981** » Seg Fev 02, 2015 21:25

Amigos, eu não consegui resolver essa. Vi na internet que 1o. Seno é a razão entre o cateto oposto a um ângulo de um triângulo retângulo e a hipotenusa. e 2o.
Função de uma variável que satisfaz a equação diferencial y"+y=0 e, que para x=0, a função e sua derivada tomam os valores 0 e 1 respectivamente.
Só que não me ajudou muito... Vocês poderiam me dar essa força.

(U.F.RS-1984) A negação da proposição "Para todo y, existe um x tal que y = sen(x)" é:

A) Para todo y, exite um x tal que y = sen(x).

B) Para todo y e para todo x, y = sen(x).

C) Existe um y e existe um x tal que y = sen(x).

D) Existe um y tal que, para todo x, y = sen(x).

E) Existe um y tal que, para todo x, y $\neq$ sen(x).

por **Russman** » Ter Fev 03, 2015 19:25

A função $f(x) = \sin(x)$ é limitada superior e inferiormente por

e

, respectivamente. Assim, o domínio de f(x)

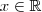é $x \in \mathbb{R}$ e sua imagem é $x \in [ -1,1 \right ]$ .

Portanto, não é verdade que para todo y real existe um x tal que $y= \sin(x)$ . Por exemplo, não existe nenhum x 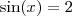real tal que $\sin(x) = 2$ .

por **adauto martins** » Qui Fev 05, 2015 11:40

algebra das proposiçoes...
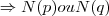N(p e q) $\Rightarrow N(p) ou N(q)$ ,onde N(negaçao)...
p=p/todo y,existe x...N(p)=p/um dado y,nao existe x...
q=y=senx...N(q)= $y\neq senx$ ...
entao dentre as alternativas dadas a q. melhor se adequa ao exposto acima seria a letra e)

Problema de lógica envolvendo Seno

Problema de lógica envolvendo Seno

Problema de lógica envolvendo Seno

Re: Problema de lógica envolvendo Seno

Re: Problema de lógica envolvendo Seno

Quem está online