 por bianca725 » Qua Fev 04, 2015 08:19
por bianca725 » Qua Fev 04, 2015 08:19
No edital de um concurso público que vou fazer. Encontra-se o seguinte tópico:
4- Relações e funções;
O que significa isso? Essas duas palavras juntas formam uma matéria? Ou terei que estudar funções, e depois relações... Estou com MUITA dúvida por favor me explique.
-
bianca725
- Novo Usuário

-
- Mensagens: 1
- Registrado em: Qua Fev 04, 2015 08:11
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Tecnico em Administração
- Andamento: formado
 por adauto martins » Qua Fev 04, 2015 18:13
por adauto martins » Qua Fev 04, 2015 18:13
para saber sobre relaçao e bom saber sobre produto cartesiano...
1)produto cartesiano:dados
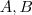
conjuntos numericos,algebricos...
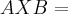
{
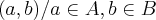
},ou seja e o conjuntos de todos os pares ordenados (a,b)...
2)relaçao:
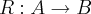
e qquer subconjuto de
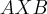
3)funçao:

eh qquer relaçao q. associa todo elemento de

a um unico elemento de

-
adauto martins
- Colaborador Voluntário

-
- Mensagens: 1171
- Registrado em: Sex Set 05, 2014 19:37
- Formação Escolar: EJA
- Área/Curso: matematica
- Andamento: cursando
Voltar para Funções
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Sistemas Lineares: "a, b e c" como "soluções".
por allendy » Qua Set 08, 2010 20:28
- 2 Respostas
- 11298 Exibições
- Última mensagem por allendy

Qua Set 08, 2010 20:37
Sistemas de Equações
-
- [LIMITES] Limite de Raiz "m" de "infinito"
por antonelli2006 » Sáb Set 17, 2011 05:56
- 5 Respostas
- 9183 Exibições
- Última mensagem por LuizAquino

Dom Set 18, 2011 10:08
Cálculo: Limites, Derivadas e Integrais
-
- (ESPCEX)duvida ""besta"'
por natanskt » Sex Nov 26, 2010 17:32
- 3 Respostas
- 4240 Exibições
- Última mensagem por DanielFerreira

Qua Dez 01, 2010 17:07
Matrizes e Determinantes
-
- Matriz constituida de "uns" e "zeros"
por Carolziiinhaaah » Qui Jun 24, 2010 12:08
- 2 Respostas
- 5736 Exibições
- Última mensagem por Carolziiinhaaah

Qui Jun 24, 2010 12:50
Matrizes e Determinantes
-
- Duvida , não consigo prosseguir com o calculo"Help"
por klysman » Ter Mai 01, 2012 20:38
- 5 Respostas
- 2499 Exibições
- Última mensagem por DanielFerreira

Qua Mai 02, 2012 23:10
Geometria Analítica
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
Exercicios de polinomios
Autor:
shaft - Qua Jun 30, 2010 17:30

Então, o exercicio pede para encontrar

.
Bom, tentei resolver a questão acima desenvolvendo as duas partes em ( )...Logo dps cheguei em um resultado q nao soube o q fazer mais.
Se vcs puderem ajudar !
Assunto:
Exercicios de polinomios
Autor:
Douglasm - Qua Jun 30, 2010 17:53
Bom, se desenvolvermos isso, encontramos:

Para que os polinômios sejam iguais, seus respectivos coeficientes devem ser iguais (ax = bx ; ax² = bx², etc.):


Somando a primeira e a segunda equação:

Finalmente:

Até a próxima.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


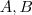 conjuntos numericos,algebricos...
conjuntos numericos,algebricos...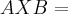 {
{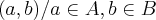 },ou seja e o conjuntos de todos os pares ordenados (a,b)...
},ou seja e o conjuntos de todos os pares ordenados (a,b)...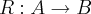 e qquer subconjuto de
e qquer subconjuto de 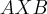
 eh qquer relaçao q. associa todo elemento de
eh qquer relaçao q. associa todo elemento de  a um unico elemento de
a um unico elemento de 


 .
.



