 por Bruna_Ferreira » Seg Jan 05, 2015 16:18
por Bruna_Ferreira » Seg Jan 05, 2015 16:18
Como eu consigo resolver esse exercício???
Existe um grupo G, de ordem 4, com geradores x e y tais que x^2=y^2=e xy=yx. Determine todos os subgrupos de G. Mostre que G={e, x, y, xy}.
-
Bruna_Ferreira
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Seg Jan 05, 2015 16:01
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Bacharelado em Matemática
- Andamento: cursando
 por adauto martins » Sex Jan 09, 2015 16:05
por adauto martins » Sex Jan 09, 2015 16:05
G e um grupo abeliano isomorfo a
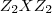
,e nao isomorfo a
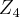
(prove como exercicio),pois
![x.y=y.x...\left[x \right]=\left[y \right]= x.y=y.x...\left[x \right]=\left[y \right]=](/latexrender/pictures/99eb78b12b08c4810379193c04ddc518.png)
{
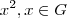
}={

}...logo <G>={

}
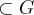
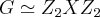
(prove como exercicio)...
sejam

,o q. e possivel pois

e
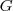
sao abelianos,G por hipotese...entao
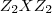
={
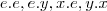
}={

}={e,x,y,xy}
-
adauto martins
- Colaborador Voluntário

-
- Mensagens: 1171
- Registrado em: Sex Set 05, 2014 19:37
- Formação Escolar: EJA
- Área/Curso: matematica
- Andamento: cursando
Voltar para Álgebra Elementar
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Teoria de grupos
por Luiz Augusto Prado » Seg Mai 30, 2011 21:37
- 1 Respostas
- 1394 Exibições
- Última mensagem por Luiz Augusto Prado

Ter Mai 31, 2011 19:21
Álgebra Elementar
-
- [Teoria dos Grupos] Derivar Teorema
por Imscatman » Qua Fev 19, 2014 18:46
- 1 Respostas
- 1166 Exibições
- Última mensagem por Imscatman

Qui Fev 20, 2014 00:11
Lógica
-
- Demonstrações
por anamendes » Sáb Abr 28, 2012 13:02
- 1 Respostas
- 1208 Exibições
- Última mensagem por LuizAquino

Sáb Abr 28, 2012 14:29
Trigonometria
-
- [complexos] demonstrações
por alentejana » Ter Mai 22, 2012 16:22
- 7 Respostas
- 3493 Exibições
- Última mensagem por joaofonseca

Ter Mai 22, 2012 20:25
Números Complexos
-
- Demonstrações Duvidas
por Razoli » Qui Ago 08, 2013 22:35
- 1 Respostas
- 1126 Exibições
- Última mensagem por e8group

Sex Ago 09, 2013 10:23
Álgebra Linear
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Funções
Autor:
Emilia - Sex Dez 03, 2010 13:24
Preciso de ajuda no seguinte problema:
O governo de um Estado Brasileiro mudou a contribuição previdenciária de seus contribuintes. era de 6% sobre qualquer salário; passou para 11% sobre o que excede R$1.200,00 nos salários. Por exemplo, sobre uma salário de R$1.700,00, a contribuição anterior era: 0,06x R$1.700,00 = R$102,00; e a atual é: 0,11x(R$1.700,00 - R$1.200,00) = R$55,00.
i. Determine as funções que fornecem o valor das contribuições em função do valor x do salário antes e depois da mudança na forma de cobrança.
ii. Esboce seus gráficos.
iii. Determine os valores de salários para os quais:
- a contribuição diminuiu;
- a contribuição permaneceu a mesma;
- a contribuição aumentou.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



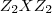 ,e nao isomorfo a
,e nao isomorfo a 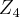 (prove como exercicio),pois
(prove como exercicio),pois ![x.y=y.x...\left[x \right]=\left[y \right]= x.y=y.x...\left[x \right]=\left[y \right]=](/latexrender/pictures/99eb78b12b08c4810379193c04ddc518.png) {
{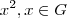 }={
}={ }...logo <G>={
}...logo <G>={ }
}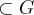
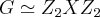 (prove como exercicio)...
(prove como exercicio)... ,o q. e possivel pois
,o q. e possivel pois  e
e 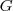 sao abelianos,G por hipotese...entao
sao abelianos,G por hipotese...entao 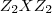 ={
={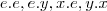 }={
}={ }={e,x,y,xy}
}={e,x,y,xy}