Alguém poderia mostrar como se chegou a essa igualdade? Não a entendi. É uma passagem de um exercício de funções de duas variáveis aleatórias.
![\int_{-\infty}^{\infty}\left[\frac{d}{dz}\int_{-\infty}^{z-x}f_{XY}(x,y)dy\right]dx=\int_{-\infty}^{\infty}f_{XY}(x,z-x)dx \int_{-\infty}^{\infty}\left[\frac{d}{dz}\int_{-\infty}^{z-x}f_{XY}(x,y)dy\right]dx=\int_{-\infty}^{\infty}f_{XY}(x,z-x)dx](/latexrender/pictures/eaeeab1ab797ff823bcd4fccb45baf44.png)
Obrigado!

![\int_{-\infty}^{\infty}\left[\frac{d}{dz}\int_{-\infty}^{z-x}f_{XY}(x,y)dy\right]dx=\int_{-\infty}^{\infty}f_{XY}(x,z-x)dx \int_{-\infty}^{\infty}\left[\frac{d}{dz}\int_{-\infty}^{z-x}f_{XY}(x,y)dy\right]dx=\int_{-\infty}^{\infty}f_{XY}(x,z-x)dx](/latexrender/pictures/eaeeab1ab797ff823bcd4fccb45baf44.png)

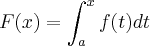 . Então F é derivável e F'(x) = f(x).
. Então F é derivável e F'(x) = f(x).
 ,pois podemos fazer como se segue:
,pois podemos fazer como se segue: ,regra de leibinitz...
,regra de leibinitz...![I=\int_{-\infty}^{z-x}\partial F(x,y)=F(x,y)[-\infty,z-x]=F(x,z-x)-F(x,-\infty) I=\int_{-\infty}^{z-x}\partial F(x,y)=F(x,y)[-\infty,z-x]=F(x,z-x)-F(x,-\infty)](/latexrender/pictures/96ce2e4b496bf5c88bc5bc1d418fd5db.png) ,sem uma definiçao de F(x,y) nada podemos concluir com
,sem uma definiçao de F(x,y) nada podemos concluir com 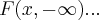

![x\in\left[a, \right b] x\in\left[a, \right b]](/latexrender/pictures/18ec34837b9a94e30aab70ad4a837bda.png) , então
, então 

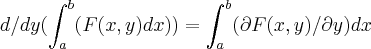 ,desde de q. F(x,y)seja continua e diferenciavel em (a,b)...qto ao exercicio e o erro...
,desde de q. F(x,y)seja continua e diferenciavel em (a,b)...qto ao exercicio e o erro...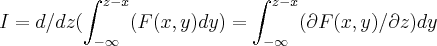 ,meu erro foi
,meu erro foi  ,mas persiste o problema do limite p/
,mas persiste o problema do limite p/

 ,
,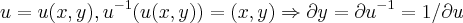

![I=\int_{u(-\infty}^{z-x}(\partial F).(\partial y/\partial u)=\int_{-\infty}^{z-x}(\partial F(x,y))=F(x,y)[-\infty,z-x]=F(x,z-x)-F(x,-\infty) I=\int_{u(-\infty}^{z-x}(\partial F).(\partial y/\partial u)=\int_{-\infty}^{z-x}(\partial F(x,y))=F(x,y)[-\infty,z-x]=F(x,z-x)-F(x,-\infty)](/latexrender/pictures/1232d771317899eb18bcc77fe9adf72b.png) ,q.recai na situaçao anterior...para q.
,q.recai na situaçao anterior...para q. 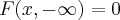 ,F tem q. ser uma funçao tipo
,F tem q. ser uma funçao tipo 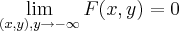

Voltar para Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 4 visitantes