 por Pessoa Estranha » Sáb Mar 08, 2014 19:30
por Pessoa Estranha » Sáb Mar 08, 2014 19:30
Olá, pessoal!
Bem, há dois exemplos dados em sala de aula e que não entendi.
Por favor, ajudem!
1 - "Consideremos
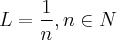
(sem o zero). Tal conjunto é limitado inferiormente, mas não tem mínimo".
2 - "Consideremos
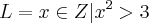
. Tal conjunto não é limitado inferiormente e não tem mínimo."
Para mim, o exemplo 1 está errado. Porque está certo?
Já no exemplo 2, eu até entendi, mas ficou uma dúvida (acho até que pode ser um absurdo): como estamos trabalhando com números inteiros, não poderia pensar que 4 é o mínimo do conjunto?
Muito Obrigada!
-
Pessoa Estranha
- Colaborador Voluntário

-
- Mensagens: 262
- Registrado em: Ter Jul 16, 2013 16:43
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
 por adauto martins » Sáb Dez 06, 2014 12:56
por adauto martins » Sáb Dez 06, 2014 12:56
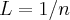
...se tomarmos o
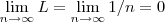
,entao 0 e o inf={1/n,
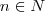
}
2)o conjunto{
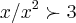
,x
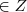
}={4,9,16,...}=
![\Rightarrow inf[4,9,16,...]=4 \Rightarrow inf[4,9,16,...]=4](/latexrender/pictures/83a34ab431df346408e53ce04420b053.png)
-
adauto martins
- Colaborador Voluntário

-
- Mensagens: 1171
- Registrado em: Sex Set 05, 2014 19:37
- Formação Escolar: EJA
- Área/Curso: matematica
- Andamento: cursando
 por adauto martins » Sáb Dez 06, 2014 15:45
por adauto martins » Sáb Dez 06, 2014 15:45
uma correçao...o conj.{4,9,16...},4 e o menor elemento do conjunto e nao a cota inferior...
-
adauto martins
- Colaborador Voluntário

-
- Mensagens: 1171
- Registrado em: Sex Set 05, 2014 19:37
- Formação Escolar: EJA
- Área/Curso: matematica
- Andamento: cursando
Voltar para Álgebra Elementar
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Estruturas algébricas
por Eliane Maria » Qua Abr 25, 2012 01:01
- 12 Respostas
- 9138 Exibições
- Última mensagem por fraol

Ter Mai 01, 2012 23:42
Álgebra Elementar
-
- Anéis ( Estruturas algébricas)
por Crist » Qui Mar 20, 2014 15:32
- 1 Respostas
- 2885 Exibições
- Última mensagem por adauto martins

Seg Mar 14, 2016 19:47
Teoria dos Números
-
- [Estruturas algébricas] Anéis
por Crist » Sáb Mar 22, 2014 16:45
- 1 Respostas
- 2084 Exibições
- Última mensagem por adauto martins

Ter Jan 13, 2015 15:45
Álgebra Elementar
-
- [Estruturas Algébricas] Relações
por Pessoa Estranha » Ter Abr 29, 2014 18:28
- 1 Respostas
- 1790 Exibições
- Última mensagem por adauto martins

Sex Dez 05, 2014 17:53
Álgebra Elementar
-
- [Estruturas Algébricas] Funções
por Pessoa Estranha » Sáb Ago 23, 2014 18:01
- 2 Respostas
- 1871 Exibições
- Última mensagem por Pessoa Estranha

Dom Ago 24, 2014 12:29
Álgebra Elementar
Usuários navegando neste fórum: Nenhum usuário registrado e 3 visitantes
Assunto:
(FGV) ... função novamente rs
Autor:
my2009 - Qua Dez 08, 2010 21:48
Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
Assunto:
(FGV) ... função novamente rs
Autor: Anonymous - Qui Dez 09, 2010 17:25
Uma função de 1º grau é dada por

.
Temos que para

,

e para

,

.

Ache o valor de

e

, monte a função e substitua

por

.
Assunto:
(FGV) ... função novamente rs
Autor:
Pinho - Qui Dez 16, 2010 13:57
my2009 escreveu:Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
f(x)= 2.x
f(3)=2.3=6
f(4)=2.4=8
f(10)=2.10=20
Assunto:
(FGV) ... função novamente rs
Autor:
dagoth - Sex Dez 17, 2010 11:55
isso ai foi uma questao da FGV?
haahua to precisando trocar de faculdade.
Assunto:
(FGV) ... função novamente rs
Autor:
Thiago 86 - Qua Mar 06, 2013 23:11
Saudações!

ví suaquestão e tentei resolver, depois você conta-me se eu acertei.
Uma função de 1º grau é dada por y=3a+b
Resposta :
3a+b=6 x(4)
4a+b=8 x(-3)
12a+4b=24
-12a-3b=-24
b=0
substituindo b na 1°, ttenho que: 3a+b=6
3a+0=6
a=2
substituindo em: y=3a+b
y=30+0
y=30

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
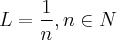 (sem o zero). Tal conjunto é limitado inferiormente, mas não tem mínimo".
(sem o zero). Tal conjunto é limitado inferiormente, mas não tem mínimo".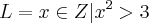 . Tal conjunto não é limitado inferiormente e não tem mínimo."
. Tal conjunto não é limitado inferiormente e não tem mínimo."

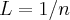 ...se tomarmos o
...se tomarmos o 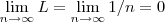 ,entao 0 e o inf={1/n,
,entao 0 e o inf={1/n,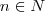 }
}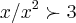 ,x
,x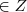 }={4,9,16,...}=
}={4,9,16,...}=![\Rightarrow inf[4,9,16,...]=4 \Rightarrow inf[4,9,16,...]=4](/latexrender/pictures/83a34ab431df346408e53ce04420b053.png)
 .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.
