 por Texorras » Sáb Jan 09, 2010 14:20
por Texorras » Sáb Jan 09, 2010 14:20
x^3
------------
3 + x^4
Se alguem me puder ajudar ( -------- e o traço de fracçao)
-
Texorras
- Novo Usuário

-
- Mensagens: 5
- Registrado em: Sáb Jan 09, 2010 13:07
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Informatica
- Andamento: cursando
 por Molina » Sáb Jan 09, 2010 15:05
por Molina » Sáb Jan 09, 2010 15:05
Boa tarde.
Faça uma substituição:
Chame
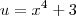
, com isso,
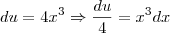
Consegue seguir agora?

Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por Hel » Sáb Jan 09, 2010 15:10
por Hel » Sáb Jan 09, 2010 15:10
Alguém pode me ajudar a resolver o gráfico f(x)= x/ln(x)
..

f´(x) = (g´(x)*h(x) - g(x)*h´(x))/(h(x))^2 = 0
..
f´(x) = ((x´)*(ln(x)) - (x)*(ln´(x)))/ln^2(x) = 0
f´(x) = (1*ln(x) - x*(1/x))/ln^2(x) = 0
f´(x) = (ln(x) - 1)/ln^2(x) = 0
..
(ln(x) - 1)/ln^2(x) = 0
ln(x) - 1 = 0
ln(x) = 1
log(x) na base e = 1
x = e
..
Não sei se esse ponto é máximo ou mínimo.
-
Hel
- Novo Usuário

-
- Mensagens: 6
- Registrado em: Sex Jan 08, 2010 20:09
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática
- Andamento: cursando
 por Texorras » Sáb Jan 09, 2010 15:11
por Texorras » Sáb Jan 09, 2010 15:11
sim .. vai dar
1/4 log(3+x^4) certo ?
-
Texorras
- Novo Usuário

-
- Mensagens: 5
- Registrado em: Sáb Jan 09, 2010 13:07
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Informatica
- Andamento: cursando
 por Hel » Sáb Jan 09, 2010 15:13
por Hel » Sáb Jan 09, 2010 15:13
Alguém pode me ajudar a resolver o gráfico f(x)= x/ln(x)
1- onde ela é decrescente e crescente;
2- mínimo e o máximo da função;
3- assíntotas
4- onde côncava e convexa
f´(x) = (g´(x)*h(x) - g(x)*h´(x))/(h(x))^2 = 0
..
f´(x) = ((x´)*(ln(x)) - (x)*(ln´(x)))/ln^2(x) = 0
f´(x) = (1*ln(x) - x*(1/x))/ln^2(x) = 0
f´(x) = (ln(x) - 1)/ln^2(x) = 0
..
(ln(x) - 1)/ln^2(x) = 0
ln(x) - 1 = 0
ln(x) = 1
log(x) na base e = 1
x = e
..
-
Hel
- Novo Usuário

-
- Mensagens: 6
- Registrado em: Sex Jan 08, 2010 20:09
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática
- Andamento: cursando
 por Molina » Sáb Jan 09, 2010 15:32
por Molina » Sáb Jan 09, 2010 15:32
Boa tarde, Hel.
Por favor, respeite as regras. Crie um tópico novo para sua dúvida e não utilize um tópico de outra questão para postar a sua. Assim o fórum fica mais organizado e fica arquivado sua dúvida no local certo.
Qualquer dúvida me procure.
Faça bom uso so fórum! 
Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por Molina » Sáb Jan 09, 2010 15:35
por Molina » Sáb Jan 09, 2010 15:35
Texorras escreveu:sim .. vai dar
1/4 log(3+x^4) certo ?
Isso mesmo.
Bom estudo,

Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por Hel » Sáb Jan 09, 2010 15:47
por Hel » Sáb Jan 09, 2010 15:47
Desculpe Diego é o meu segundo acesso.
Att,
Helmar
-
Hel
- Novo Usuário

-
- Mensagens: 6
- Registrado em: Sex Jan 08, 2010 20:09
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Calculo de uma Primitiva
por Texorras » Sáb Jan 09, 2010 13:13
- 7 Respostas
- 4440 Exibições
- Última mensagem por Douglasm

Dom Abr 11, 2010 19:23
Cálculo: Limites, Derivadas e Integrais
-
- primitiva
por rodrigonapoleao » Qua Jan 02, 2013 14:34
- 1 Respostas
- 1629 Exibições
- Última mensagem por young_jedi

Qua Jan 02, 2013 17:37
Cálculo: Limites, Derivadas e Integrais
-
- primitiva
por Ana Maria da Silva » Sáb Nov 23, 2013 13:37
- 1 Respostas
- 1468 Exibições
- Última mensagem por e8group

Sáb Nov 23, 2013 20:33
Cálculo: Limites, Derivadas e Integrais
-
- primitiva
por Ana Maria da Silva » Qui Nov 28, 2013 11:23
- 1 Respostas
- 1555 Exibições
- Última mensagem por Bravim

Sex Nov 29, 2013 00:14
Cálculo: Limites, Derivadas e Integrais
-
- primitiva
por bebelo32 » Sáb Mar 21, 2015 20:52
- 1 Respostas
- 2041 Exibições
- Última mensagem por adauto martins

Dom Mar 22, 2015 13:29
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 3 visitantes
Assunto:
Exercicios de polinomios
Autor:
shaft - Qua Jun 30, 2010 17:30

Então, o exercicio pede para encontrar

.
Bom, tentei resolver a questão acima desenvolvendo as duas partes em ( )...Logo dps cheguei em um resultado q nao soube o q fazer mais.
Se vcs puderem ajudar !
Assunto:
Exercicios de polinomios
Autor:
Douglasm - Qua Jun 30, 2010 17:53
Bom, se desenvolvermos isso, encontramos:

Para que os polinômios sejam iguais, seus respectivos coeficientes devem ser iguais (ax = bx ; ax² = bx², etc.):


Somando a primeira e a segunda equação:

Finalmente:

Até a próxima.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



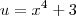 , com isso,
, com isso, 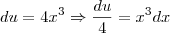












 .
.



