 por Pessoa Estranha » Qua Nov 26, 2014 17:49
por Pessoa Estranha » Qua Nov 26, 2014 17:49
Olá, pessoal! Gostaria de saber se a minha resolução está certa.
O exercício pede para encontrar

, tal que
![\sqrt[]{\frac{\overline {11}}{\overline 5}} + \overline 2x = \overline 4 \sqrt[]{\frac{\overline {11}}{\overline 5}} + \overline 2x = \overline 4](/latexrender/pictures/273570a5af134d7eca431ed0f52062c4.png)
.
![\sqrt[]{\frac{\overline {11}}{\overline 5}} = b \Rightarrow b + \overline 2x = \overline 4 \Rightarrow b = \overline 4 - \overline 2x \sqrt[]{\frac{\overline {11}}{\overline 5}} = b \Rightarrow b + \overline 2x = \overline 4 \Rightarrow b = \overline 4 - \overline 2x](/latexrender/pictures/83ac1971811b0400ba814c9cd7b44f8f.png)
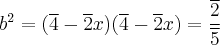
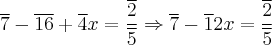
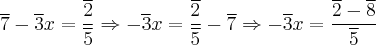

Está certo? Ou fiz tudo errado?
Fiquei na dúvida com relação ao que fazer com

.

-
Pessoa Estranha
- Colaborador Voluntário

-
- Mensagens: 262
- Registrado em: Ter Jul 16, 2013 16:43
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
Voltar para Álgebra Elementar
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Estruturas Algébricas] Classes Laterais
por Pessoa Estranha » Sáb Nov 22, 2014 17:47
- 0 Respostas
- 1011 Exibições
- Última mensagem por Pessoa Estranha

Sáb Nov 22, 2014 17:47
Álgebra Elementar
-
- Estruturas algébricas
por Eliane Maria » Qua Abr 25, 2012 01:01
- 12 Respostas
- 9165 Exibições
- Última mensagem por fraol

Ter Mai 01, 2012 23:42
Álgebra Elementar
-
- Anéis ( Estruturas algébricas)
por Crist » Qui Mar 20, 2014 15:32
- 1 Respostas
- 2890 Exibições
- Última mensagem por adauto martins

Seg Mar 14, 2016 19:47
Teoria dos Números
-
- [Estruturas algébricas] Anéis
por Crist » Sáb Mar 22, 2014 16:45
- 1 Respostas
- 2087 Exibições
- Última mensagem por adauto martins

Ter Jan 13, 2015 15:45
Álgebra Elementar
-
- [Estruturas Algébricas] Relações
por Pessoa Estranha » Ter Abr 29, 2014 18:28
- 1 Respostas
- 1794 Exibições
- Última mensagem por adauto martins

Sex Dez 05, 2014 17:53
Álgebra Elementar
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
cálculo de limites
Autor:
Hansegon - Seg Ago 25, 2008 11:29
Bom dia.
Preciso de ajuda na solução deste problema, pois só chego ao resultado de 0 sobre 0.
Obrigado
\lim_{x\rightarrow-1} x³ +1/x²-1[/tex]
Assunto:
cálculo de limites
Autor:
Molina - Seg Ago 25, 2008 13:25

Realmente se você jogar o -1 na equação dá 0 sobre 0.
Indeterminações deste tipo você pode resolver por L'Hôpital
que utiliza derivada.
Outro modo é transformar o numerador e/ou denominador
para que não continue dando indeterminado.
Dica: dividir o numerador e o denominador por algum valor é uma forma que normalmente dá certo.

Caso ainda não tenha dado uma

, avisa que eu resolvo.
Bom estudo!
Assunto:
cálculo de limites
Autor:
Guill - Dom Abr 08, 2012 16:03



Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 , tal que
, tal que ![\sqrt[]{\frac{\overline {11}}{\overline 5}} + \overline 2x = \overline 4 \sqrt[]{\frac{\overline {11}}{\overline 5}} + \overline 2x = \overline 4](/latexrender/pictures/273570a5af134d7eca431ed0f52062c4.png) .
.![\sqrt[]{\frac{\overline {11}}{\overline 5}} = b \Rightarrow b + \overline 2x = \overline 4 \Rightarrow b = \overline 4 - \overline 2x \sqrt[]{\frac{\overline {11}}{\overline 5}} = b \Rightarrow b + \overline 2x = \overline 4 \Rightarrow b = \overline 4 - \overline 2x](/latexrender/pictures/83ac1971811b0400ba814c9cd7b44f8f.png)
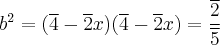
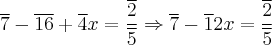
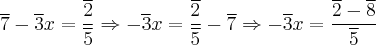

 .
. 

 , tal que
, tal que ![\sqrt[]{\frac{\overline {11}}{\overline 5}} + \overline 2x = \overline 4 \sqrt[]{\frac{\overline {11}}{\overline 5}} + \overline 2x = \overline 4](/latexrender/pictures/273570a5af134d7eca431ed0f52062c4.png) .
.![\sqrt[]{\frac{\overline {11}}{\overline 5}} = b \Rightarrow b + \overline 2x = \overline 4 \Rightarrow b = \overline 4 - \overline 2x \sqrt[]{\frac{\overline {11}}{\overline 5}} = b \Rightarrow b + \overline 2x = \overline 4 \Rightarrow b = \overline 4 - \overline 2x](/latexrender/pictures/83ac1971811b0400ba814c9cd7b44f8f.png)
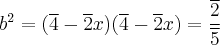
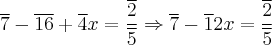
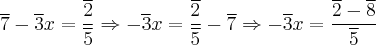

 .
. 

![\sqrt[]{({11})^{-}.{(({5})^{-1}})^{-}}+{2}^{-}x=(\sqrt[]{(11.{5}^{-1})}^-)+{2}^{-}x=\sqrt[]{{1}^{-}}+{2}^{-}x={4}^{-}\Rightarrow {1}^{-}+{2}^{-}x={4}^{-}\Rightarrow {2}^{-}x={4}^{-}+{-1}^{-} \sqrt[]{({11})^{-}.{(({5})^{-1}})^{-}}+{2}^{-}x=(\sqrt[]{(11.{5}^{-1})}^-)+{2}^{-}x=\sqrt[]{{1}^{-}}+{2}^{-}x={4}^{-}\Rightarrow {1}^{-}+{2}^{-}x={4}^{-}\Rightarrow {2}^{-}x={4}^{-}+{-1}^{-}](/latexrender/pictures/c8b8d7f83af134850f2d7904bd8e19c8.png)
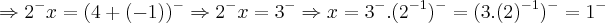 ,onde
,onde 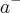 e o resto da divisao euclidiana por 9,no caso...
e o resto da divisao euclidiana por 9,no caso...


 , avisa que eu resolvo.
, avisa que eu resolvo.

