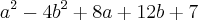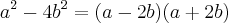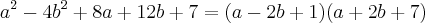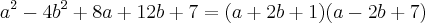por giancarlo_vanitelli » Ter Nov 25, 2014 16:22
por giancarlo_vanitelli » Ter Nov 25, 2014 16:22
Estudei todos os produtos notáveis, estudei o trinômio de Stewin, estudei um pouco como fatorar através do método de completar quadrados, porém mesmo assim há inúmeras fatorações que não faço ideia de como começar a resolver, parece que o que aprendi não é suficiente e tem algo a mais que sempre fica faltando nessa matéria (fatoração). Segue minhas tentativas de resolução de dois exercícios, peço por gentileza que apontem o que estou fazendo de errado.
Ex1) x²-4a²+6x+12a
= x(x+6)-4a(a-3)
=(x+6)(x-4)(a-3) < Minha resposta
Resposta informada no gabarito> (x+2a)(x-2a+6)
Ex2) a²-4b²+8a+12b+7
= a(a+8)-4b(b-3)+7
= (a+8)(b-3)(a-4b+7) < Minha resposta
Resposta informada no gabarito> (a+2b+1)(a-2b+7)
O que eu devo estudar para resolver este tipo de fatoração?
Desde já agradeço.
-
giancarlo_vanitelli
- Novo Usuário

-
- Mensagens: 7
- Registrado em: Sáb Nov 22, 2014 16:55
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Ciências Contábeis
- Andamento: cursando
 por nakagumahissao » Qua Nov 26, 2014 11:58
por nakagumahissao » Qua Nov 26, 2014 11:58
Exemplo 1:
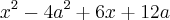
Nesta primeira, podemos observar a presença de x ao quadrado e 'a' ao quadrado. Percebemos também que esta primeira parte:

se parece muito com o formato:
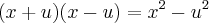
Assim, para sabermos o valor de 'u' acima, bastará que façamos:
![u^{2} = 4a^{2} \Rightarrow u = \pm \sqrt[]{4a^{2}} = \pm |2a| = \pm 2a u^{2} = 4a^{2} \Rightarrow u = \pm \sqrt[]{4a^{2}} = \pm |2a| = \pm 2a](/latexrender/pictures/efb24fd365cb292ece80028c102f2687.png)
Logo, para esta primeira parte:
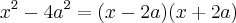
Para a segunda parte,
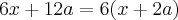
Juntando tudo, temos:
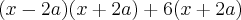
Como (x + 2a) aparece duas vezes, podemos colocá-lo em evidência para termos:
![(x+2a)[(x - 2a) + 6] = (x+2a)(x - 2a + 6) (x+2a)[(x - 2a) + 6] = (x+2a)(x - 2a + 6)](/latexrender/pictures/0546fabbc1466f3178447671e6ca9baf.png)
Que é a resposta desejada para este primeiro exemplo.
Eu faço a diferença. E você?
Do Poema: Quanto os professores "fazem"?
De Taylor Mali
-
nakagumahissao
- Colaborador Voluntário

-
- Mensagens: 386
- Registrado em: Qua Abr 04, 2012 14:07
- Localização: Brazil
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Lic. Matemática
- Andamento: cursando
-
 por nakagumahissao » Qua Nov 26, 2014 16:14
por nakagumahissao » Qua Nov 26, 2014 16:14
Para a situação do
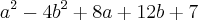
Note que:
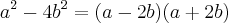
e que 7 somente poderá ser produzido por 7 vezes 1. Assim
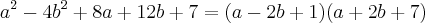
ou
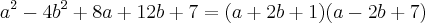
tanto faz.
Eu faço a diferença. E você?
Do Poema: Quanto os professores "fazem"?
De Taylor Mali
-
nakagumahissao
- Colaborador Voluntário

-
- Mensagens: 386
- Registrado em: Qua Abr 04, 2012 14:07
- Localização: Brazil
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Lic. Matemática
- Andamento: cursando
-
 por giancarlo_vanitelli » Qua Nov 26, 2014 18:36
por giancarlo_vanitelli » Qua Nov 26, 2014 18:36
Obrigado Nakagumahissao,
há algum método a ser utilizado nesse tipo de fatoração (2° caso) ou o mesmo apenas pode resolvido através da logica msm? Tenho bastante dificuldade neste tipo de fatoração.
-
giancarlo_vanitelli
- Novo Usuário

-
- Mensagens: 7
- Registrado em: Sáb Nov 22, 2014 16:55
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Ciências Contábeis
- Andamento: cursando
 por nakagumahissao » Qua Nov 26, 2014 19:28
por nakagumahissao » Qua Nov 26, 2014 19:28
Não veja uma forma mais fácil a não ser um pouco de criatividade em cada situação dessas.
Eu faço a diferença. E você?
Do Poema: Quanto os professores "fazem"?
De Taylor Mali
-
nakagumahissao
- Colaborador Voluntário

-
- Mensagens: 386
- Registrado em: Qua Abr 04, 2012 14:07
- Localização: Brazil
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Lic. Matemática
- Andamento: cursando
-
Voltar para Álgebra Elementar
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Fatoração] O que estou fazendo de errado?
por giancarlo_vanitelli » Sáb Nov 22, 2014 19:02
- 3 Respostas
- 1735 Exibições
- Última mensagem por DanielFerreira

Dom Nov 23, 2014 21:47
Álgebra Elementar
-
- [Fatoração] O que estou fazendo de errado?
por giancarlo_vanitelli » Ter Nov 25, 2014 15:57
- 1 Respostas
- 1656 Exibições
- Última mensagem por DanielFerreira

Sáb Dez 13, 2014 15:25
Álgebra Elementar
-
- O que estou fazendo errado
por micheli57 » Seg Mar 02, 2015 21:47
- 2 Respostas
- 2197 Exibições
- Última mensagem por micheli57

Ter Mar 03, 2015 09:06
Álgebra Elementar
-
- O que estou fazendo errado
por micheli57 » Seg Mar 02, 2015 21:57
- 1 Respostas
- 1647 Exibições
- Última mensagem por Russman

Seg Mar 02, 2015 22:56
Álgebra Elementar
-
- [INEQUAÇÕES] O que estou fazendo de errado?
por homerbrasil » Qua Jan 11, 2012 16:44
- 5 Respostas
- 2903 Exibições
- Última mensagem por homerbrasil

Qui Jan 12, 2012 16:28
Polinômios
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 12:41
pessoal eu achei como resultado 180 toneladas,entretanto sei que a questão está erra pela lógica e a resposta correta segundo o gabarito é 1.800 toneladas.
me explique onde eu estou pecando na questão. resolva explicando.
78 – ( CEFET – 1993 ) Os desabamentos, em sua maioria, são causados por grande acúmulo de lixo nas encostas dos morros. Se 10 pessoas retiram 135 toneladas de lixo em 9 dias, quantas toneladas serão retiradas por 40 pessoas em 30 dias ?
Assunto:
dúvida em uma questão em regra de 3!
Autor:
Douglasm - Qui Jul 01, 2010 13:16
Observe o raciocínio:
10 pessoas - 9 dias - 135 toneladas
1 pessoa - 9 dias - 13,5 toneladas
1 pessoa - 1 dia - 1,5 toneladas
40 pessoas - 1 dia - 60 toneladas
40 pessoas - 30 dias - 1800 toneladas
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:18
pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:21
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
valeu meu camarada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


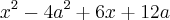

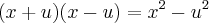
![u^{2} = 4a^{2} \Rightarrow u = \pm \sqrt[]{4a^{2}} = \pm |2a| = \pm 2a u^{2} = 4a^{2} \Rightarrow u = \pm \sqrt[]{4a^{2}} = \pm |2a| = \pm 2a](/latexrender/pictures/efb24fd365cb292ece80028c102f2687.png)
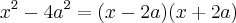
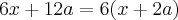
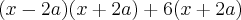
![(x+2a)[(x - 2a) + 6] = (x+2a)(x - 2a + 6) (x+2a)[(x - 2a) + 6] = (x+2a)(x - 2a + 6)](/latexrender/pictures/0546fabbc1466f3178447671e6ca9baf.png)