por Pessoa Estranha » Ter Nov 18, 2014 00:38
![\sqrt[5]{x-2}](/latexrender/pictures/3077b32665829a49219836be64d5ac4d.png "\sqrt[5]{x-2}")
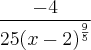. Daí, não há pontos reais para os quais a derivada segunda da f se anula. Contudo, x = 2 está no domínio da f e é, realmente, a abscissa do ponto de inflexão, mas como chegar neste resultado usando as derivadas e sem observar o gráfico da f? Pq não deu certo?
por adauto martins » Qua Nov 19, 2014 11:46
![f(x)=\sqrt[5]{x-2}=0\Rightarrow x=2](/latexrender/pictures/ea0c85a502ea218a13a208284cf1a0ff.png "f(x)=\sqrt[5]{x-2}=0\Rightarrow x=2")
,x=2 e o ponto onde f,cruza o eixo xx...![df/dx=(1/5)1/(\sqrt[5]{{x-2}^{4}})=0\Rightarrow](/latexrender/pictures/dfb72ab60de1da46a82ae0ce046cfa4a.png "df/dx=(1/5)1/(\sqrt[5]{{x-2}^{4}})=0\Rightarrow")
nao existem pontos nem de maximos e minimos,mas a funçao e crescente,pois 
,p/ qquer x do dominio,
...![({df/dx})^{2}=(-4/25)(\sqrt[5]{({x-2})^{9}})=0](/latexrender/pictures/2c0f115f91028ad44ed6806e741b495c.png "({df/dx})^{2}=(-4/25)(\sqrt[5]{({x-2})^{9}})=0")
q. nao tem concavidades...portanto f e uma funçao sem pontos criticos,mas cresce indefinidamente,pois ![\lim_{x\rightarrow\infty}(\sqrt[5]{x-2})=\infty](/latexrender/pictures/12ec7e0fbcdd23d3bd585d69a80a9dfc.png "\lim_{x\rightarrow\infty}(\sqrt[5]{x-2})=\infty")
...por trickpsv » Sex Nov 21, 2014 16:06
por adauto martins » Sex Nov 21, 2014 17:01
Voltar para Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 3 visitantes
, avisa que eu resolvo.
