Calcular integral usando método da substituição simples por U:
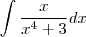
Resposta:
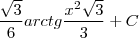
Tentei fazer e me perdi todo. Porque eu comecei fazendo assim:
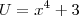
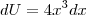
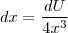
Ai substituí e ficou:
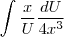, coloquei os números para fora e cortei um X, dai ficou: 
, onde achei que o du/u daria lnu, então finalmente ficou 
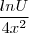, ai coloquei o valor de U no lugar e cheguei no resultado: 
, o que é bem diferente da resposta que tem na apostila. Agradeço quem puder deixar o passo a passo bem detalhado, pq estou perdido mesmo, e pelo jeito sem saber como fazer :(