Estou com dúvidas num exercício.
"Prove que:
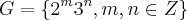 e
e 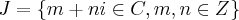 são subgrupos de, respectivamente,
são subgrupos de, respectivamente, 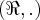 e
e 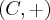 . Prove que G e J são isomorfos."
. Prove que G e J são isomorfos."Provar que são subgrupos eu consegui. O problema está na segunda parte, provar que G e J são isomorfos. Não precisamos de uma aplicação f: G -> J definida por uma lei e tal que devemos mostrar que é homomorfismo de grupos e, depois, que é bijetora? Se não, como posso resolver isto sem uma lei definida?
Muito Obrigada!


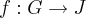 tal q.
tal q.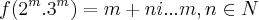 ...temos q. mostrar q. f e bijetiva e homomorfica de subgrupos G,J...
...temos q. mostrar q. f e bijetiva e homomorfica de subgrupos G,J...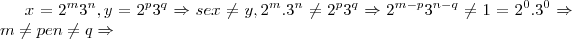
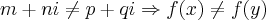 ,logo f e injetiva...
,logo f e injetiva...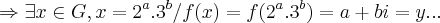 f e sobrejetiva,logo f e bijetiva...
f e sobrejetiva,logo f e bijetiva...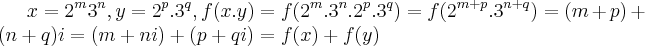 q. e um homomorfismo de subgrupos...
q. e um homomorfismo de subgrupos...![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
 e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)