 por EREGON » Seg Nov 10, 2014 21:02
por EREGON » Seg Nov 10, 2014 21:02
Olá,
agradeço a vossa ajuda para perceber o seguinte exercício:
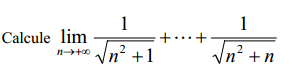
- Limites_Sucessões.PNG (4.98 KiB) Exibido 7800 vezes
é errado afirmar que o limite desta sucessão tende para 0, atendendo à grandeza do denominador? Existe alguma descrição matemática para a resolução deste tipo de exercícios?
Obrigado,
Paulo
-
EREGON
- Usuário Ativo

-
- Mensagens: 12
- Registrado em: Seg Nov 10, 2014 16:00
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: informatica
- Andamento: cursando
 por adauto martins » Ter Nov 11, 2014 14:09
por adauto martins » Ter Nov 11, 2014 14:09
![L=\lim_{n\rightarrow\infty}\sum_{1}^{n}(1/\sqrt[]{{n}^{2}-n})=\lim_{n\rightarrow\infty}\sum_{1}^{n}(1/({n}^{2})(1/\sqrt[]{1-1/(n)} L=\lim_{n\rightarrow\infty}\sum_{1}^{n}(1/\sqrt[]{{n}^{2}-n})=\lim_{n\rightarrow\infty}\sum_{1}^{n}(1/({n}^{2})(1/\sqrt[]{1-1/(n)}](/latexrender/pictures/b4e161dea3ed1bbb420a0f5ba63a2be3.png)
=
![\sum_{1}^{n}\lim_{n\rightarrow\infty}(1/({n}^{2})).\lim_{n\rightarrow\infty}1/(\sqrt[]{1-1/n})=\sum_{1}^{n}0.1=0 \sum_{1}^{n}\lim_{n\rightarrow\infty}(1/({n}^{2})).\lim_{n\rightarrow\infty}1/(\sqrt[]{1-1/n})=\sum_{1}^{n}0.1=0](/latexrender/pictures/a3b6aab9807ab0b74f675e87649b581d.png)
...
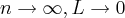
...esse exercicio e para determinar se uma sucessao ,ou uma serie converge...e estudar sequencias e series,calculo 2,ou3...na verdade p/sequencias ou serie...vc toma o limite do termo geral,p/verificar se converge ou nao...termo geral eh:
![1/(\sqrt[]{({n})^{2}-n} 1/(\sqrt[]{({n})^{2}-n}](/latexrender/pictures/aa14bab1b60fe4ed7e23944739eff1a2.png)
-
adauto martins
- Colaborador Voluntário

-
- Mensagens: 1171
- Registrado em: Sex Set 05, 2014 19:37
- Formação Escolar: EJA
- Área/Curso: matematica
- Andamento: cursando
 por e8group » Ter Nov 11, 2014 23:38
por e8group » Ter Nov 11, 2014 23:38
Acredito que o limite seja 1 ... vejamos , fixado

arbitrariamente , temos
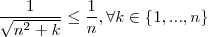
.Daí ,
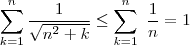
. Por outro lado ,

, implicando
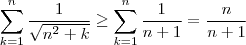
.
Desta forma,

. A conclusão do limite valer 1 segue de
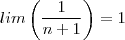
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por adauto martins » Qua Nov 12, 2014 12:39
por adauto martins » Qua Nov 12, 2014 12:39
santiago vc novamente,
primeiro vc entra em uma questao minha e da bola fora...sobre subespaços,dizendo q. o vetorv=(...) e subespaço...q. no caso,nao eh...existem dois subespaços triviais(vetor nulo e o proprio espaço) e qquer outro subespaço tem q. conter a origem...agora vem querendo me contradizer...estude mais matematica...primeiramente

,caso q. nao se tem como reduzir a uma forma elementar,usando algebrismos de limites...e outra

diverge,por ser serie harmonica ,o q. refuta seus argumentos...
-
adauto martins
- Colaborador Voluntário

-
- Mensagens: 1171
- Registrado em: Sex Set 05, 2014 19:37
- Formação Escolar: EJA
- Área/Curso: matematica
- Andamento: cursando
 por adauto martins » Qua Nov 12, 2014 19:58
por adauto martins » Qua Nov 12, 2014 19:58
uma correçao,o limite da serie em questao,diverge p/infinito...correçao:
![L=\lim_{x\rightarrow\infty}\sum_{1}^{n}(1/(\sqrt[]{{n}^{2}+n})=\sum_{1}^{\infty}(1/(\sqrt[]{{n}^{2}+n}) \preceq \sum_{1}^{\infty}(1/(\sqrt[]{{n}^{2}})=\sum_{1}^{\infty}(1/n)=\infty L=\lim_{x\rightarrow\infty}\sum_{1}^{n}(1/(\sqrt[]{{n}^{2}+n})=\sum_{1}^{\infty}(1/(\sqrt[]{{n}^{2}+n}) \preceq \sum_{1}^{\infty}(1/(\sqrt[]{{n}^{2}})=\sum_{1}^{\infty}(1/n)=\infty](/latexrender/pictures/6c3005a4f28f15e562e79794ae4cbb67.png)
...obrigado
-
adauto martins
- Colaborador Voluntário

-
- Mensagens: 1171
- Registrado em: Sex Set 05, 2014 19:37
- Formação Escolar: EJA
- Área/Curso: matematica
- Andamento: cursando
 por e8group » Qui Nov 13, 2014 12:05
por e8group » Qui Nov 13, 2014 12:05
Caro adauto martins , calma ! Por favor , só estou aqui para expor minha opinião , não estou criticando vc e etc ... Equívocos absolutamente é normal .. A respeito do tópico sobre o subespaço veja o mesmo novamente .
No meu ponto de vista , não faz sentido a divergência da serie p/ infitnity , muito menos a convergência da mesma para zero .
Note que

percorre de

até

, com

grande o quanto vc queira . Desta forma
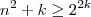
(pois estamos a trabalhar com n arbitrariamente grande ) , e disso vem que
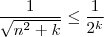
[meu novo argumento ) , logo ( pois estamos estamos no corpo dos reais , e a relação " <=" é compatível com a adição )
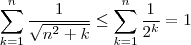
. E trivialmente podemos limitar inferiormente

por 0 , e por este argumento não diverge p/ infinity .
Fazendo ,
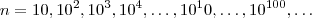
de acordo com o wolframalhpa .... temos respectivamente
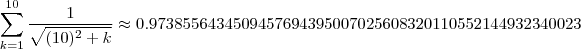
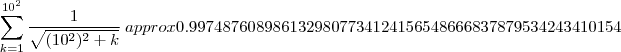
(...)
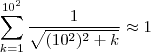
(...)

Expectativa :

.
Porém para estudantes de matemática e qq um que gosta de mat , certamente o argumento acima não é válido ... Se alguém aí conseguir formalizar faça o favor de postar .
É isso !
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por adauto martins » Qui Nov 13, 2014 14:27
por adauto martins » Qui Nov 13, 2014 14:27
meu caro santiago,
primeiramente a serie

e uma serie geometrica cuja soma e infinita,q. se calcula como se segue:

=1/(1-r),
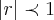
,r=1/2
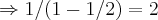
...calculo q. vc errou...qto as series

sao ditas series harmonicas q. convergem p/
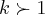
e divergem p/
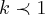
(fato bom de se provar...) o q. vejo e q. vc conhece pouco de calculo,pois isso q. escrevi acima e a nivel de calculo2,3...q. se faz em graduaçao dos cursos de ciencias basicas e exatas,engenharias etc...bom,estamos sempre sujeitos a erros,eu mesmo vi q. errei na questao pelo fato de estar calculando muitos limites aqui,e me sequeci q. tal limite era um limite de uma serie infinita...mas vim e consertei meu erro...tbem nao quero discordia,por que estamos aqui com o mesmo fim,ajudar no melhor q. podemos as pessoas q. procuram aqui uma soluçao p/suas duvidas em matematica...sempre concordarei com argumentos melhores q. o meu,se caso eu esteja errado...
-
adauto martins
- Colaborador Voluntário

-
- Mensagens: 1171
- Registrado em: Sex Set 05, 2014 19:37
- Formação Escolar: EJA
- Área/Curso: matematica
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Conclusão sobre Limite de sucessões
 por EREGON » Sex Nov 14, 2014 15:00
por EREGON » Sex Nov 14, 2014 15:00
- 2 Respostas
- 3902 Exibições
- Última mensagem por EREGON

Seg Nov 17, 2014 13:19
Cálculo: Limites, Derivadas e Integrais
-
- sucessões
por joanafrancisca » Ter Jul 24, 2012 23:23
- 2 Respostas
- 2261 Exibições
- Última mensagem por joanafrancisca

Qua Jul 25, 2012 01:53
Cálculo: Limites, Derivadas e Integrais
-
- sucessoes
por ulisses123 » Sex Jun 20, 2014 15:23
- 7 Respostas
- 5526 Exibições
- Última mensagem por e8group

Dom Jul 06, 2014 16:11
Sequências
-
- Limities sucessões
por matpet92 » Qui Fev 02, 2012 22:13
- 4 Respostas
- 3658 Exibições
- Última mensagem por matpet92

Dom Fev 05, 2012 20:29
Cálculo: Limites, Derivadas e Integrais
-
- Limites de Funções vs Sucessões
por joaofonseca » Seg Mai 02, 2011 22:56
- 1 Respostas
- 2346 Exibições
- Última mensagem por LuizAquino

Seg Mai 02, 2011 23:09
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Proporcionalidade
Autor:
silvia fillet - Qui Out 13, 2011 22:46
Divida o numero 35 em partes diretamente proporcionais a 4, 10 e 14. Em seguida divida o mesmo numero em partes proporcionais a 6, 15 e 21. explique por que os resultados sao iguais.
Assunto:
Proporcionalidade
Autor:
silvia fillet - Sáb Out 15, 2011 10:25
POR GENTILEZA PODEM VERIFICAR SE O MEU RACIOCINIO ESTÁ CERTO?
P1 = K.4 SUBSTITUINDO K POR 1,25 P1= 5
P2 = K.10 SUBSTITUINDO K POR 1,25 P2= 12,50
P3 = K.13 SUBSTITUINDO K POR 1,25 P3= 17,50
P1+P2+P3 = 35
K.4+K.10+K.13 = 35
28 K = 35
K= 1,25
P1 = K.6 SUBSTITUINDO K POR 0,835 P1= 5
P2 = K.15 SUBSTITUINDO K POR 0,835 P2 = 12,50
P3 = K.21 SUBSTITUINDO K POR 0,835 P3 = 17,50
K.6+K.15+K.21 = 35
42K = 35
K= 0,833
4/6 =10/15 =14/21 RAZÃO = 2/3
SERÁ QUE ESTÁ CERTO?
ALGUEM PODE ME AJUDAR A EXPLICAR MELHOR?
OBRIGADA
SILVIA
Assunto:
Proporcionalidade
Autor:
ivanfx - Dom Out 16, 2011 00:37
utilize a definição e não se baseie no exercícios resolvidos da redefor, assim você terá mais clareza, mas acredito que sua conclusão esteja correto, pois o motivo de darem o mesmo resultado é pq a razão é a mesma.
Assunto:
Proporcionalidade
Autor:
Marcos Roberto - Dom Out 16, 2011 18:24
Silvia:
Acho que o resultado é o mesmo pq as razões dos coeficientes e as razões entre os números são inversamente proporcionais.
Você conseguiu achar o dia em que caiu 15 de novembro de 1889?
Assunto:
Proporcionalidade
Autor:
deiasp - Dom Out 16, 2011 23:45
Ola pessoal
Tb. estou no redefor
O dia da semana em 15 de novembro de 1889, acredito que foi em uma sexta feira
Assunto:
Proporcionalidade
Autor:
silvia fillet - Seg Out 17, 2011 06:23
Bom dia,
Realmente foi uma sexta feira, como fazer os calculos para chegar ?
Assunto:
Proporcionalidade
Autor:
ivanfx - Seg Out 17, 2011 07:18
Para encontrar o dia que caiu 15 de novembro de 1889 você deve em primeiro lugar encontrar a quantidade de anos bissextos que houve entre 1889 à 2011, após isso dá uma verificada no ano 1900, ele não é bissexto, pois a regra diz que ano que é múltiplo de 100 e não é múltiplo de 400 não é bissexto.
Depois calcule quantos dias dão de 1889 até 2011, basta pegar a quantidade de anos e multiplicar por 365 + 1 dia a cada ano bissexto (esse resultado você calculou quando encontrou a quantidade de anos bissextos)
Pegue o resultado e divida por 7 e vai obter o resto.
obtendo o resto e partindo da data que pegou como referência conte a quantidade do resto para trás da semana.
Assunto:
Proporcionalidade
Autor:
silvia fillet - Seg Out 17, 2011 07:40
Bom dia,
Será que é assim:
2011 a 1889 são 121 anos sendo , 30 anos bissextos e 91 anos normais então temos:
30x366 = 10.980 dias
91x365 = 33.215 dias
incluindo 15/11/1889 - 31/12/1889 47 dias
33215+10980+47 = 44242 dias
44242:7 = 6320 + resto 2
è assim, nâo sei mais sair disso.
Assunto:
Proporcionalidade
Autor:
ivanfx - Seg Out 17, 2011 10:24
que tal descontar 1 dia do seu resultado, pois 1900 não é bissexto, ai seria 44241 e quando fizer a divisão o resto será 1
como etá pegando base 1/01/2011, se reparar bem 01/01/2011 sempre cai no mesmo dia que 15/01/2011, sendo assim se 01/01/2011 caiu em um sábado volte 1 dia para trás, ou seja, você está no sábado e voltando 1 dia voltará para sexta.então 15/11/1889 cairá em uma sexta
Assunto:
Proporcionalidade
Autor:
Kiwamen2903 - Seg Out 17, 2011 19:43
Boa noite, sou novo por aqui, espero poder aprender e ajudar quando possível! A minha resposta ficou assim:
De 1889 até 2001 temos 29 anos bissextos a começar por 1892 (primeiro múltiplo de 4 após 1889) e terminar por 2008 (último múltiplo de 4 antes de 2011). Vale lembrar que o ano 1900 não é bissexto, uma vez que é múltiplo de 100 mas não é múltiplo de 400.
De um ano normal para outro, se considerarmos a mesma data, eles caem em dias consecutivos da semana. Por exemplo 01/01/2011 – sábado, e 01/01/2010 – sexta.
De um ano bissexto para outro, se considerarmos a mesma data, um cai dois dias da semana depois do outro. Por exemplo 01/01/2008 (ano bissexto) – Terça – feira, e 01/01/09 – Quinta-feira.
Sendo assim, se contarmos um dia da semana de diferença para cada um dos 01/01 dos 122 anos que separam 1889 e 2011 mais os 29 dias a mais referentes aos anos bissextos entre 1889 e 2011, concluímos que são 151 dias da semana de diferença, o que na realidade nos trás: 151:7= 21x7+4, isto é, são 4 dias da semana de diferença. Logo, como 15/11/2011 cairá em uma terça-feira, 15/11/1889 caiu em uma sexta-feira.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


![L=\lim_{n\rightarrow\infty}\sum_{1}^{n}(1/\sqrt[]{{n}^{2}-n})=\lim_{n\rightarrow\infty}\sum_{1}^{n}(1/({n}^{2})(1/\sqrt[]{1-1/(n)} L=\lim_{n\rightarrow\infty}\sum_{1}^{n}(1/\sqrt[]{{n}^{2}-n})=\lim_{n\rightarrow\infty}\sum_{1}^{n}(1/({n}^{2})(1/\sqrt[]{1-1/(n)}](/latexrender/pictures/b4e161dea3ed1bbb420a0f5ba63a2be3.png) =
=![\sum_{1}^{n}\lim_{n\rightarrow\infty}(1/({n}^{2})).\lim_{n\rightarrow\infty}1/(\sqrt[]{1-1/n})=\sum_{1}^{n}0.1=0 \sum_{1}^{n}\lim_{n\rightarrow\infty}(1/({n}^{2})).\lim_{n\rightarrow\infty}1/(\sqrt[]{1-1/n})=\sum_{1}^{n}0.1=0](/latexrender/pictures/a3b6aab9807ab0b74f675e87649b581d.png) ...
...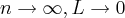 ...esse exercicio e para determinar se uma sucessao ,ou uma serie converge...e estudar sequencias e series,calculo 2,ou3...na verdade p/sequencias ou serie...vc toma o limite do termo geral,p/verificar se converge ou nao...termo geral eh:
...esse exercicio e para determinar se uma sucessao ,ou uma serie converge...e estudar sequencias e series,calculo 2,ou3...na verdade p/sequencias ou serie...vc toma o limite do termo geral,p/verificar se converge ou nao...termo geral eh:![1/(\sqrt[]{({n})^{2}-n} 1/(\sqrt[]{({n})^{2}-n}](/latexrender/pictures/aa14bab1b60fe4ed7e23944739eff1a2.png)

 arbitrariamente , temos
arbitrariamente , temos 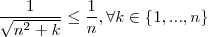 .Daí ,
.Daí , 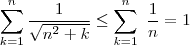 . Por outro lado ,
. Por outro lado ,  , implicando
, implicando 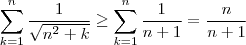 .
.  . A conclusão do limite valer 1 segue de
. A conclusão do limite valer 1 segue de 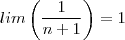
 ,caso q. nao se tem como reduzir a uma forma elementar,usando algebrismos de limites...e outra
,caso q. nao se tem como reduzir a uma forma elementar,usando algebrismos de limites...e outra  diverge,por ser serie harmonica ,o q. refuta seus argumentos...
diverge,por ser serie harmonica ,o q. refuta seus argumentos...![L=\lim_{x\rightarrow\infty}\sum_{1}^{n}(1/(\sqrt[]{{n}^{2}+n})=\sum_{1}^{\infty}(1/(\sqrt[]{{n}^{2}+n}) \preceq \sum_{1}^{\infty}(1/(\sqrt[]{{n}^{2}})=\sum_{1}^{\infty}(1/n)=\infty L=\lim_{x\rightarrow\infty}\sum_{1}^{n}(1/(\sqrt[]{{n}^{2}+n})=\sum_{1}^{\infty}(1/(\sqrt[]{{n}^{2}+n}) \preceq \sum_{1}^{\infty}(1/(\sqrt[]{{n}^{2}})=\sum_{1}^{\infty}(1/n)=\infty](/latexrender/pictures/6c3005a4f28f15e562e79794ae4cbb67.png) ...obrigado
...obrigado percorre de
percorre de  até
até 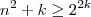 (pois estamos a trabalhar com n arbitrariamente grande ) , e disso vem que
(pois estamos a trabalhar com n arbitrariamente grande ) , e disso vem que 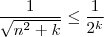 [meu novo argumento ) , logo ( pois estamos estamos no corpo dos reais , e a relação " <=" é compatível com a adição )
[meu novo argumento ) , logo ( pois estamos estamos no corpo dos reais , e a relação " <=" é compatível com a adição ) 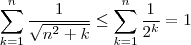 . E trivialmente podemos limitar inferiormente
. E trivialmente podemos limitar inferiormente  por 0 , e por este argumento não diverge p/ infinity .
por 0 , e por este argumento não diverge p/ infinity . 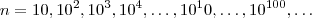 de acordo com o wolframalhpa .... temos respectivamente
de acordo com o wolframalhpa .... temos respectivamente 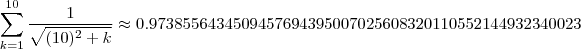
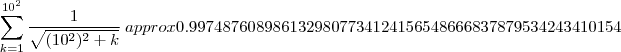
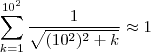

 .
. e uma serie geometrica cuja soma e infinita,q. se calcula como se segue:
e uma serie geometrica cuja soma e infinita,q. se calcula como se segue: 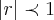 ,r=1/2
,r=1/2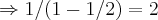 ...calculo q. vc errou...qto as series
...calculo q. vc errou...qto as series  sao ditas series harmonicas q. convergem p/
sao ditas series harmonicas q. convergem p/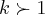 e divergem p/
e divergem p/ 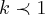 (fato bom de se provar...) o q. vejo e q. vc conhece pouco de calculo,pois isso q. escrevi acima e a nivel de calculo2,3...q. se faz em graduaçao dos cursos de ciencias basicas e exatas,engenharias etc...bom,estamos sempre sujeitos a erros,eu mesmo vi q. errei na questao pelo fato de estar calculando muitos limites aqui,e me sequeci q. tal limite era um limite de uma serie infinita...mas vim e consertei meu erro...tbem nao quero discordia,por que estamos aqui com o mesmo fim,ajudar no melhor q. podemos as pessoas q. procuram aqui uma soluçao p/suas duvidas em matematica...sempre concordarei com argumentos melhores q. o meu,se caso eu esteja errado...
(fato bom de se provar...) o q. vejo e q. vc conhece pouco de calculo,pois isso q. escrevi acima e a nivel de calculo2,3...q. se faz em graduaçao dos cursos de ciencias basicas e exatas,engenharias etc...bom,estamos sempre sujeitos a erros,eu mesmo vi q. errei na questao pelo fato de estar calculando muitos limites aqui,e me sequeci q. tal limite era um limite de uma serie infinita...mas vim e consertei meu erro...tbem nao quero discordia,por que estamos aqui com o mesmo fim,ajudar no melhor q. podemos as pessoas q. procuram aqui uma soluçao p/suas duvidas em matematica...sempre concordarei com argumentos melhores q. o meu,se caso eu esteja errado...