 por Ariel » Dom Nov 09, 2014 16:45
por Ariel » Dom Nov 09, 2014 16:45
Pessoal, entendi como se acha o valor do ângulo, mas este exercício eu não consegui resolver. Só sei q o resultado dá 40. Alguém poderia me ajudar? Desde já muito obrigada!!!
- Anexos
-

-
Ariel
- Usuário Dedicado

-
- Mensagens: 37
- Registrado em: Dom Nov 09, 2014 16:33
- Formação Escolar: ENSINO FUNDAMENTAL I
- Andamento: cursando
 por adauto martins » Seg Nov 10, 2014 10:03
por adauto martins » Seg Nov 10, 2014 10:03
o arco na circunferencia corresponde ao angulo inscrito de de 50,eh 100...do ponto oposto ao angulo de 50 ao ponto de encontro com reta q. contem o centro o,sera de 80...logo...2x=80...x=40
-
adauto martins
- Colaborador Voluntário

-
- Mensagens: 1171
- Registrado em: Sex Set 05, 2014 19:37
- Formação Escolar: EJA
- Área/Curso: matematica
- Andamento: cursando
 por Ariel » Ter Nov 11, 2014 17:14
por Ariel » Ter Nov 11, 2014 17:14
Adauto, muito obrigada! Vou ver alguém aqui pra me dizer, pois na verdade não consegui entender este ponto oposto. O ponto "O" é importante para resolver isto? Abs!
-
Ariel
- Usuário Dedicado

-
- Mensagens: 37
- Registrado em: Dom Nov 09, 2014 16:33
- Formação Escolar: ENSINO FUNDAMENTAL I
- Andamento: cursando
 por Ariel » Ter Nov 11, 2014 18:26
por Ariel » Ter Nov 11, 2014 18:26
Também não consegui resolver este:
Se alguém puder me ajudar, agradeço!
- Anexos
-

-
Ariel
- Usuário Dedicado

-
- Mensagens: 37
- Registrado em: Dom Nov 09, 2014 16:33
- Formação Escolar: ENSINO FUNDAMENTAL I
- Andamento: cursando
 por adauto martins » Ter Nov 11, 2014 19:43
por adauto martins » Ter Nov 11, 2014 19:43
cara ariel,
eu nao sei postar figuras aqui no site,entao ve-se vc consegue visualizar os pontos q. descreverei aqui,ai vc entendera a resoluçao...sejam A,B,C,D pontos sobre a circunferencia da figura,pontos de intersecçao das retas internas a circunferencia...começando em A, sentido anti-horario e vai ate D,ponto do angulo inscrito,50°...o ponto oposto ao qual me refiro eh B...todo angulo inscrito tem a metade do arco,sob a circunferencia,q. o determina...entao o arco AB=100...como a reta q. corta a circunferencia passa pelo ponto O, centro e vai ate C,tem medida de 180...como o arco AB=100, o arco BC tera 80,q. e o dobro de x...entao x=40...o outrop exercicio sera:
6x+30=2.(4x)...6x+30=8x...8x-6x=30...2x=30...x=15...espero ter esclarecido...
-
adauto martins
- Colaborador Voluntário

-
- Mensagens: 1171
- Registrado em: Sex Set 05, 2014 19:37
- Formação Escolar: EJA
- Área/Curso: matematica
- Andamento: cursando
 por Ariel » Ter Nov 11, 2014 20:43
por Ariel » Ter Nov 11, 2014 20:43
Entendi os dois agora! Muito obrigada pela atenção, Adauto!! Abs!!
-
Ariel
- Usuário Dedicado

-
- Mensagens: 37
- Registrado em: Dom Nov 09, 2014 16:33
- Formação Escolar: ENSINO FUNDAMENTAL I
- Andamento: cursando
 por Ariel » Ter Nov 11, 2014 20:48
por Ariel » Ter Nov 11, 2014 20:48
Só uma coisa: no segundo exercício o 6x+30 é o tamanho do arco tb? ABS!
-
Ariel
- Usuário Dedicado

-
- Mensagens: 37
- Registrado em: Dom Nov 09, 2014 16:33
- Formação Escolar: ENSINO FUNDAMENTAL I
- Andamento: cursando
 por adauto martins » Qua Nov 12, 2014 11:21
por adauto martins » Qua Nov 12, 2014 11:21
esse 2x-30 e o angulo central,referente ao arco...angulos e arcos tem uma relaçao comum,
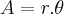
,onde A(arco,q. se mede em
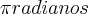
),

(angulo,central ou inscrito q. se mede em graus°)e r raio da circunferencia...os arcos sao medidas na propria circunferencia,e os angulos sao associados a eles...
-
adauto martins
- Colaborador Voluntário

-
- Mensagens: 1171
- Registrado em: Sex Set 05, 2014 19:37
- Formação Escolar: EJA
- Área/Curso: matematica
- Andamento: cursando
 por Ariel » Qua Nov 12, 2014 11:52
por Ariel » Qua Nov 12, 2014 11:52
Obrigada, Adauto!!
-
Ariel
- Usuário Dedicado

-
- Mensagens: 37
- Registrado em: Dom Nov 09, 2014 16:33
- Formação Escolar: ENSINO FUNDAMENTAL I
- Andamento: cursando
Voltar para Geometria Plana
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Angulo inscrito e arco capaz - 2
 por Ariel » Sex Nov 21, 2014 23:46
por Ariel » Sex Nov 21, 2014 23:46
- 4 Respostas
- 3029 Exibições
- Última mensagem por Ariel

Dom Nov 23, 2014 18:33
Geometria Plana
-
- quadrilátero inscrito e angulo
 por alfabeta » Dom Mar 04, 2012 21:33
por alfabeta » Dom Mar 04, 2012 21:33
- 2 Respostas
- 4268 Exibições
- Última mensagem por alfabeta

Seg Mar 05, 2012 11:22
Geometria Plana
-
- [Ângulo para um dado arco e raio] Dedução e compreensão.
por Matheus Lacombe O » Dom Nov 11, 2012 21:49
- 3 Respostas
- 3290 Exibições
- Última mensagem por MarceloFantini

Seg Nov 12, 2012 19:53
Trigonometria
-
- [Ângulo/circunferência] Ângulo CÂB, ajude-me!
 por miltonsermoud » Qua Set 30, 2015 17:14
por miltonsermoud » Qua Set 30, 2015 17:14
- 3 Respostas
- 3502 Exibições
- Última mensagem por miltonsermoud

Sex Out 02, 2015 07:41
Geometria Plana
-
- arco
por cristina » Ter Set 22, 2009 15:03
- 2 Respostas
- 1561 Exibições
- Última mensagem por cristina

Ter Set 22, 2009 23:45
Trigonometria
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
Funções
Autor:
Emilia - Sex Dez 03, 2010 13:24
Preciso de ajuda no seguinte problema:
O governo de um Estado Brasileiro mudou a contribuição previdenciária de seus contribuintes. era de 6% sobre qualquer salário; passou para 11% sobre o que excede R$1.200,00 nos salários. Por exemplo, sobre uma salário de R$1.700,00, a contribuição anterior era: 0,06x R$1.700,00 = R$102,00; e a atual é: 0,11x(R$1.700,00 - R$1.200,00) = R$55,00.
i. Determine as funções que fornecem o valor das contribuições em função do valor x do salário antes e depois da mudança na forma de cobrança.
ii. Esboce seus gráficos.
iii. Determine os valores de salários para os quais:
- a contribuição diminuiu;
- a contribuição permaneceu a mesma;
- a contribuição aumentou.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.









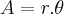 ,onde A(arco,q. se mede em
,onde A(arco,q. se mede em 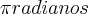 ),
), (angulo,central ou inscrito q. se mede em graus°)e r raio da circunferencia...os arcos sao medidas na propria circunferencia,e os angulos sao associados a eles...
(angulo,central ou inscrito q. se mede em graus°)e r raio da circunferencia...os arcos sao medidas na propria circunferencia,e os angulos sao associados a eles...
