 por Cleyson007 » Dom Nov 09, 2014 09:19
por Cleyson007 » Dom Nov 09, 2014 09:19
Gostaria de saber se a resolução está correta.
A temperatura em um ponto (x,y,z) é dado por

onde T é medido em graus Celsius e x, y e z em metros.
a) Determine a taxa de variação da temperatura no ponto (2, -1, 2) em direção ao ponto (3, -3, 3).
Pensei assim:
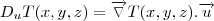
![\overrightarrow{\triangledown}T(x,y,z)=200\left [ (-2x\,e^{-x^2-3y^2-9z^2})i+(-6y\, e^{-x^2-3y^2-9z^2})j + (-18z\,e^{-x^2-3y^2-9z^2})k \right ] \overrightarrow{\triangledown}T(x,y,z)=200\left [ (-2x\,e^{-x^2-3y^2-9z^2})i+(-6y\, e^{-x^2-3y^2-9z^2})j + (-18z\,e^{-x^2-3y^2-9z^2})k \right ]](/latexrender/pictures/af07c403b2e4667ea5500466d8ca0d89.png)

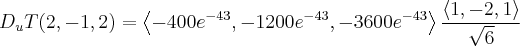
Resolvendo,

-

Cleyson007
- Colaborador Voluntário

-
- Mensagens: 1228
- Registrado em: Qua Abr 30, 2008 00:08
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática UFJF
- Andamento: formado
 por adauto martins » Sáb Dez 27, 2014 19:02
por adauto martins » Sáb Dez 27, 2014 19:02

)...
p/ o gradiente o vetor

-
adauto martins
- Colaborador Voluntário

-
- Mensagens: 1171
- Registrado em: Sex Set 05, 2014 19:37
- Formação Escolar: EJA
- Área/Curso: matematica
- Andamento: cursando
 por Cleyson007 » Ter Mai 05, 2015 15:21
por Cleyson007 » Ter Mai 05, 2015 15:21
Não entendi essa resolução sua amigo.
Na verdade, eu gostaria de saber a minha resolução está correta.
Abraço
-

Cleyson007
- Colaborador Voluntário

-
- Mensagens: 1228
- Registrado em: Qua Abr 30, 2008 00:08
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática UFJF
- Andamento: formado
 por adauto martins » Ter Mai 05, 2015 19:17
por adauto martins » Ter Mai 05, 2015 19:17
caro colega cleyson...
erro muito em fazer calculo(contas),mas seu desenvolvimento esta sim correto...
-
adauto martins
- Colaborador Voluntário

-
- Mensagens: 1171
- Registrado em: Sex Set 05, 2014 19:37
- Formação Escolar: EJA
- Área/Curso: matematica
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Taxa de variação
por felipe_ad » Ter Jun 29, 2010 19:44
- 2 Respostas
- 60613 Exibições
- Última mensagem por Guill

Ter Fev 21, 2012 21:17
Cálculo: Limites, Derivadas e Integrais
-
- Taxa de variação
 por AlbertoAM » Sáb Mai 21, 2011 14:23
por AlbertoAM » Sáb Mai 21, 2011 14:23
- 1 Respostas
- 5495 Exibições
- Última mensagem por LuizAquino

Dom Mai 22, 2011 13:03
Cálculo: Limites, Derivadas e Integrais
-
- Taxa de Variação
 por AlbertoAM » Sáb Mai 28, 2011 15:53
por AlbertoAM » Sáb Mai 28, 2011 15:53
- 10 Respostas
- 10639 Exibições
- Última mensagem por AlbertoAM

Ter Mai 31, 2011 21:32
Cálculo: Limites, Derivadas e Integrais
-
- Taxa de Variação
 por Pollyanna Moraes » Sáb Out 22, 2011 17:37
por Pollyanna Moraes » Sáb Out 22, 2011 17:37
- 1 Respostas
- 8463 Exibições
- Última mensagem por LuizAquino

Dom Out 23, 2011 10:15
Cálculo: Limites, Derivadas e Integrais
-
- taxa de variacao
por cal12 » Dom Nov 27, 2011 16:46
- 3 Respostas
- 5404 Exibições
- Última mensagem por Russman

Sex Jun 29, 2012 22:01
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 6 visitantes
Assunto:
Unesp - 95 Números Complexos
Autor:
Alucard014 - Dom Ago 01, 2010 18:22
(UNESP - 95) Seja L o Afixo de um Número complexo

em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
Assunto:
Unesp - 95 Números Complexos
Autor:
MarceloFantini - Qui Ago 05, 2010 17:27
Seja

o ângulo entre o eixo horizontal e o afixo

. O triângulo é retângulo com catetos

e

, tal que

. Seja

o ângulo complementar. Então

. Como

, o ângulo que o afixo

formará com a horizontal será

, mas negativo pois tem de ser no quarto quadrante. Se

, então

. Como módulo é um:

.
Logo, o afixo é

.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 onde T é medido em graus Celsius e x, y e z em metros.
onde T é medido em graus Celsius e x, y e z em metros.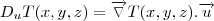
![\overrightarrow{\triangledown}T(x,y,z)=200\left [ (-2x\,e^{-x^2-3y^2-9z^2})i+(-6y\, e^{-x^2-3y^2-9z^2})j + (-18z\,e^{-x^2-3y^2-9z^2})k \right ] \overrightarrow{\triangledown}T(x,y,z)=200\left [ (-2x\,e^{-x^2-3y^2-9z^2})i+(-6y\, e^{-x^2-3y^2-9z^2})j + (-18z\,e^{-x^2-3y^2-9z^2})k \right ]](/latexrender/pictures/af07c403b2e4667ea5500466d8ca0d89.png)

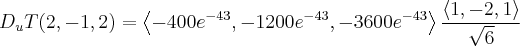


 onde T é medido em graus Celsius e x, y e z em metros.
onde T é medido em graus Celsius e x, y e z em metros.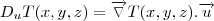
![\overrightarrow{\triangledown}T(x,y,z)=200\left [ (-2x\,e^{-x^2-3y^2-9z^2})i+(-6y\, e^{-x^2-3y^2-9z^2})j + (-18z\,e^{-x^2-3y^2-9z^2})k \right ] \overrightarrow{\triangledown}T(x,y,z)=200\left [ (-2x\,e^{-x^2-3y^2-9z^2})i+(-6y\, e^{-x^2-3y^2-9z^2})j + (-18z\,e^{-x^2-3y^2-9z^2})k \right ]](/latexrender/pictures/af07c403b2e4667ea5500466d8ca0d89.png)

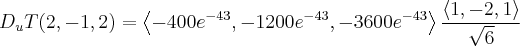


 )...
)...



 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , mas negativo pois tem de ser no quarto quadrante. Se
, mas negativo pois tem de ser no quarto quadrante. Se  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.