Olá, estou em dúvida sobre qual operadora de cartão de crédito utilizar. Na verdade já sei mais ou menos o resultado, mas fiz o processo por chute (também conhecido como iteração hipotética rsrs). Gostaria de saber qual o cálculo correto. Os dados são os seguintes:
Bandeira A:
R$ 192,00 mensais (aluguel máquina cartões)
4% de taxa por transação (crédito parcelado)
Bandeira B:
R$ 12,00 mensais (aluguel máquina cartões)
7% de taxa por transação (crédito parcelado)
-----------------
Meu cálculo:
Através do meu método "empírico" fiz o seguinte:
Custo fixo: R$ 192,00 - R$ 12,00: Diferença de custos fixos: R$ 180,00
Custo variável: R$ 7% - 4% = Diferença de custo variável: 3%
Baseado nisto, fui chutando até encontrar que quando eu estiver movimentando R$ 6.000 em transações, as duas ficam equivalentes. Antes disto a máquina B é melhor, e depois deste valor a máquina A é melhor. Cheguei nisto tentando descobrir qual o valor de transações corresponderia aos 3% de diferença entre uma e outra.
3% de 6.000 = 180 reais
(R$ 6.000*4%)+180= R$ 420
(R$ 6.000*7%)+12 = R$ 432
---------------------------------------------
Por favor, me ensinem uma formula matemática para fazer este tipo de cálculo


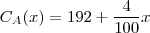
 .
. de transações efetuadas for tal que
de transações efetuadas for tal que  . O contrário será
. O contrário será 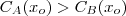 , onde é mais econômico usar a bandeira B. A economia será nula se
, onde é mais econômico usar a bandeira B. A economia será nula se  .
. ,
, 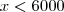 e
e  .
. é a função economia, então
é a função economia, então  de modo que
de modo que 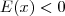 significa ser mais econômico usar a bandeira A,
significa ser mais econômico usar a bandeira A,  significa igualdade de custos e
significa igualdade de custos e 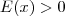 significa ser mais econômico usar a bandeira B.
significa ser mais econômico usar a bandeira B. de modo que
de modo que 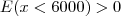 ,
,  e
e 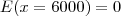 .
.
