Reduza a expressão dada em um único logaritmo:
log9 x + log3 6 - 3log9 z
Me ajudem por favor



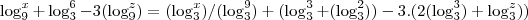 =
=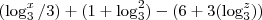 =
=![(\log_{3}^{x}/3)-3\log_{3}^{z}+\log_{3}^{2}-5=\log_{3}^{2(\sqrt[3]{x})/(({z}^{3})(\sqrt[5]{3}))} (\log_{3}^{x}/3)-3\log_{3}^{z}+\log_{3}^{2}-5=\log_{3}^{2(\sqrt[3]{x})/(({z}^{3})(\sqrt[5]{3}))}](/latexrender/pictures/322c56424442435d43bc951946b3289a.png) ...costumo errar em contas,mas o racionio e esse...confere ai
...costumo errar em contas,mas o racionio e esse...confere ai

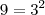 de modo que, segundo a identidade
de modo que, segundo a identidade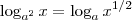
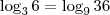 .
.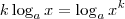 . Portanto,
. Portanto, 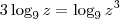 . Assim, sua expressão fica
. Assim, sua expressão fica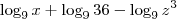

Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes

 .
.
 :
: