


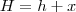 , onde
, onde 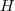 é a altura da TV com relação ao solo e
é a altura da TV com relação ao solo e  a altura dos olhos da pessoa om relação ao mesmo.. Portanto, uma vez calculado
a altura dos olhos da pessoa om relação ao mesmo.. Portanto, uma vez calculado  seremos capazes de calcular
seremos capazes de calcular 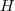 . Assim, nossa busca será o de calcular o ângulo
. Assim, nossa busca será o de calcular o ângulo  em função de
em função de  a fim de estudar a correspondente maximização.
a fim de estudar a correspondente maximização. 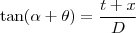 da mesma maneira que
da mesma maneira que 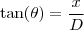 . Assim, como
. Assim, como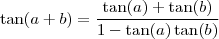
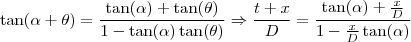
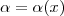 ) é
) é 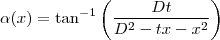
 extremiza
extremiza 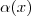 se
se 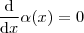 . Assim, como
. Assim, como 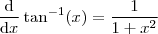 então, aplicando a regra da cadeia, vem que
então, aplicando a regra da cadeia, vem que
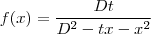 .
.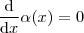 implica em
implica em 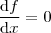 já que
já que 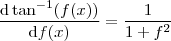 nunca se anula.
nunca se anula.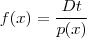 onde
onde 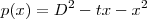 . Assim, para calcular a solução de
. Assim, para calcular a solução de 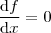 basta tomar
basta tomar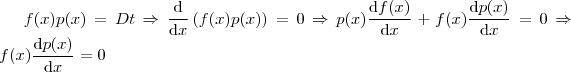
 nunca se anula a solução vem com
nunca se anula a solução vem com 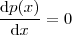 . Ou seja,
. Ou seja, 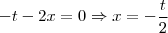
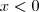 mostra que a TV deve estar a uma altura menor do que a propria altura dos olhos do assistente.
mostra que a TV deve estar a uma altura menor do que a propria altura dos olhos do assistente.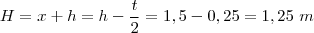 .
.
Voltar para Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 9 visitantes