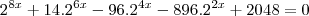
RESP.(-2,15)

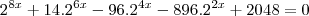

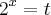

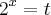 para encontrar os valores de x.
para encontrar os valores de x.
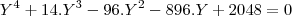
 ,P(Y) e polinomio com coeficientes inteiros,logo existe p/q,tais q. p,q sao primos entre si,P(p/q)=0,onde p e divisor de 2048,q divisor de 1,ou seja P(p)=0,p e divisor de 2048...D(2048)={1,
,P(Y) e polinomio com coeficientes inteiros,logo existe p/q,tais q. p,q sao primos entre si,P(p/q)=0,onde p e divisor de 2048,q divisor de 1,ou seja P(p)=0,p e divisor de 2048...D(2048)={1,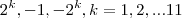 ,
, {-8,-16,2,8},como p=Y=
{-8,-16,2,8},como p=Y=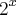 ,logo os p
,logo os p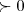 ,entao Y=p=2,8
,entao Y=p=2,8 x=1/2 e x=3/2...logo S={1/2,3/2}
x=1/2 e x=3/2...logo S={1/2,3/2}
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes

 .
.



