 por ALPC » Qui Set 18, 2014 18:28
por ALPC » Qui Set 18, 2014 18:28
Olá, eu estava lendo um livro quando me deparei com a seguinte dúvida:
Conjunto Vazio
![F = \left[\,x \,| \,x \,\in \, $\mathbb{Z}$ \, e \:x^2 \:+ 1 \,= \,\,0\right]] F = \left[\,x \,| \,x \,\in \, $\mathbb{Z}$ \, e \:x^2 \:+ 1 \,= \,\,0\right]]](/latexrender/pictures/d4f2e795300c9fede3b8aa3f370ca35a.png)
pelo que eu entendi, ele está dizendo que para o x pertencer ao conjunto F, é preciso que ele pertença aos números inteiros e que ao ser elevado ao quadrado e ser somado com 1 fique 0.
Pela minha interpretação, ao falar que esse conjunto é vazio, não existe nenhum número que ao passar pelos procedimentos acima se torne 0. Mas então eu pensei:
-1 pertence aos números inteiros então:
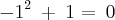
o livro que está errado ou é meu raciocínio ?
-

ALPC
- Usuário Ativo

-
- Mensagens: 19
- Registrado em: Sex Jan 04, 2013 16:26
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por DanielFerreira » Sex Set 19, 2014 14:53
por DanielFerreira » Sex Set 19, 2014 14:53
ALPC,
boa tarde!
Vejamos,
![\\ x^2 + 1 = 0 \\\\ x^2 = - 1 \\\\ x = \sqrt[2]{- 1} \\\\ (...) \\ x^2 + 1 = 0 \\\\ x^2 = - 1 \\\\ x = \sqrt[2]{- 1} \\\\ (...)](/latexrender/pictures/82511f06534b2299cd66c79bee546db2.png)
Em se tratando de números complexos, poderíamos prosseguir; entretanto, "x" pertence aos inteiros! Daí, o conjunto é VAZIO!
Quanto ao raciocínio,...
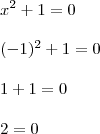
Que é falso!
"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação

-
- Mensagens: 1732
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Mangaratiba - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
 por ALPC » Sex Set 19, 2014 17:46
por ALPC » Sex Set 19, 2014 17:46
obrigado danjr5, agora vi que errei ali na potenciação
-

ALPC
- Usuário Ativo

-
- Mensagens: 19
- Registrado em: Sex Jan 04, 2013 16:26
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por DanielFerreira » Dom Set 21, 2014 13:51
por DanielFerreira » Dom Set 21, 2014 13:51
Não há de quê!
"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação

-
- Mensagens: 1732
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Mangaratiba - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
 por adauto martins » Seg Set 22, 2014 13:04
por adauto martins » Seg Set 22, 2014 13:04
z\in Z,entao z=x+yi,onde x,y sao reais...como nao se tem soluçao real para {x}^{2}+1=0,logo F e vazio...
-
adauto martins
- Colaborador Voluntário

-
- Mensagens: 1171
- Registrado em: Sex Set 05, 2014 19:37
- Formação Escolar: EJA
- Área/Curso: matematica
- Andamento: cursando
 por adauto martins » Seg Set 22, 2014 15:44
por adauto martins » Seg Set 22, 2014 15:44

,eita num sei usar esse editor,mas e isso num tem xao quadradop ,mais yao quadrado mais um igual a zero,nao existe sol.real...deu pra entender...
-
adauto martins
- Colaborador Voluntário

-
- Mensagens: 1171
- Registrado em: Sex Set 05, 2014 19:37
- Formação Escolar: EJA
- Área/Curso: matematica
- Andamento: cursando
Voltar para Conjuntos
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Dúvida iniciante sobre conjuntos
por cassiosv13 » Sex Mar 09, 2012 01:45
- 1 Respostas
- 1652 Exibições
- Última mensagem por cassiosv13

Sex Mar 09, 2012 02:14
Conjuntos
-
- Dúvida sobre operações entre conjuntos - complementar
por Fernanda Lauton » Sáb Out 09, 2010 21:18
- 3 Respostas
- 2624 Exibições
- Última mensagem por MarceloFantini

Sáb Out 09, 2010 23:18
Funções
-
- Problema sobre Conjuntos.
 por Vinicius » Dom Abr 05, 2009 17:12
por Vinicius » Dom Abr 05, 2009 17:12
- 4 Respostas
- 4503 Exibições
- Última mensagem por Vinicius

Dom Abr 05, 2009 22:17
Conjuntos
-
- Questao sobre conjuntos
por cadu » Ter Out 19, 2010 23:16
- 0 Respostas
- 1447 Exibições
- Última mensagem por cadu

Ter Out 19, 2010 23:16
Álgebra Elementar
-
- Questão do ITA sobre conjuntos!
por Abelardo » Qui Mar 03, 2011 02:03
- 5 Respostas
- 5426 Exibições
- Última mensagem por LuizAquino

Sex Mar 04, 2011 09:44
Álgebra Elementar
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
cálculo de limites
Autor:
Hansegon - Seg Ago 25, 2008 11:29
Bom dia.
Preciso de ajuda na solução deste problema, pois só chego ao resultado de 0 sobre 0.
Obrigado
\lim_{x\rightarrow-1} x³ +1/x²-1[/tex]
Assunto:
cálculo de limites
Autor:
Molina - Seg Ago 25, 2008 13:25

Realmente se você jogar o -1 na equação dá 0 sobre 0.
Indeterminações deste tipo você pode resolver por L'Hôpital
que utiliza derivada.
Outro modo é transformar o numerador e/ou denominador
para que não continue dando indeterminado.
Dica: dividir o numerador e o denominador por algum valor é uma forma que normalmente dá certo.

Caso ainda não tenha dado uma

, avisa que eu resolvo.
Bom estudo!
Assunto:
cálculo de limites
Autor:
Guill - Dom Abr 08, 2012 16:03



Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![F = \left[\,x \,| \,x \,\in \, $\mathbb{Z}$ \, e \:x^2 \:+ 1 \,= \,\,0\right]] F = \left[\,x \,| \,x \,\in \, $\mathbb{Z}$ \, e \:x^2 \:+ 1 \,= \,\,0\right]]](/latexrender/pictures/d4f2e795300c9fede3b8aa3f370ca35a.png)
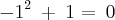


![\\ x^2 + 1 = 0 \\\\ x^2 = - 1 \\\\ x = \sqrt[2]{- 1} \\\\ (...) \\ x^2 + 1 = 0 \\\\ x^2 = - 1 \\\\ x = \sqrt[2]{- 1} \\\\ (...)](/latexrender/pictures/82511f06534b2299cd66c79bee546db2.png)
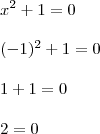


 ,eita num sei usar esse editor,mas e isso num tem xao quadradop ,mais yao quadrado mais um igual a zero,nao existe sol.real...deu pra entender...
,eita num sei usar esse editor,mas e isso num tem xao quadradop ,mais yao quadrado mais um igual a zero,nao existe sol.real...deu pra entender...

 , avisa que eu resolvo.
, avisa que eu resolvo.

