 por rodrigoboreli » Dom Set 07, 2014 00:52
por rodrigoboreli » Dom Set 07, 2014 00:52
Boa noite meus amigos, sou novato no forum, mas preciso muito da ajuda de vocês.
Consegui chegar até na metade deste exercício e gostaria da ajuda de vocês para termina-lo.
Ex. Mostrar que a função y =
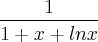
satisfaz a equação xy' = y (y ln x - 1).
Até onde consegui fazer:
y =
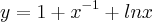
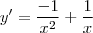
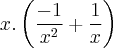
=
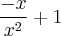
=
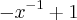
isso tem que ser = y (y ln x - 1).
Depois disso eu empaquei e não consegui igualar com essa parte: y (y ln x - 1).
Por favor vejam se meu raciocínio esta certo, me ajudem!! preciso entregar isso no final da semana que vem, obrigado desde já!
-
rodrigoboreli
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Dom Set 07, 2014 00:28
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia da Computação
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Números que satisfaz a equação
por Lucio » Qua Out 17, 2012 12:16
- 2 Respostas
- 1176 Exibições
- Última mensagem por Lucio

Qua Out 17, 2012 21:22
Equações
-
- [Derivada]Mostrar uma expressão.
por amigao » Dom Mai 26, 2013 21:28
- 1 Respostas
- 1075 Exibições
- Última mensagem por e8group

Dom Mai 26, 2013 22:02
Cálculo: Limites, Derivadas e Integrais
-
- [FUNÇÃO PAR E ÍMPAR] Mostrar uma verdade absoluta
por samifel » Qui Abr 12, 2012 17:07
- 1 Respostas
- 1934 Exibições
- Última mensagem por MarceloFantini

Qui Abr 12, 2012 19:25
Funções
-
- Nao consigo mostrar
por 380625 » Sáb Jun 02, 2012 16:42
- 1 Respostas
- 1152 Exibições
- Última mensagem por Russman

Sáb Jun 02, 2012 17:52
Cálculo: Limites, Derivadas e Integrais
-
- [Derivada] Ajuda com calculo de derivada de função quociente
por alienpuke » Dom Out 25, 2015 15:31
- 1 Respostas
- 12556 Exibições
- Última mensagem por Cleyson007

Dom Out 25, 2015 16:47
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
cálculo de limites
Autor:
Hansegon - Seg Ago 25, 2008 11:29
Bom dia.
Preciso de ajuda na solução deste problema, pois só chego ao resultado de 0 sobre 0.
Obrigado
\lim_{x\rightarrow-1} x³ +1/x²-1[/tex]
Assunto:
cálculo de limites
Autor:
Molina - Seg Ago 25, 2008 13:25

Realmente se você jogar o -1 na equação dá 0 sobre 0.
Indeterminações deste tipo você pode resolver por L'Hôpital
que utiliza derivada.
Outro modo é transformar o numerador e/ou denominador
para que não continue dando indeterminado.
Dica: dividir o numerador e o denominador por algum valor é uma forma que normalmente dá certo.

Caso ainda não tenha dado uma

, avisa que eu resolvo.
Bom estudo!
Assunto:
cálculo de limites
Autor:
Guill - Dom Abr 08, 2012 16:03



Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
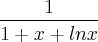 satisfaz a equação xy' = y (y ln x - 1).
satisfaz a equação xy' = y (y ln x - 1).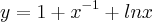
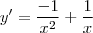
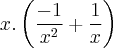
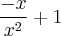
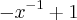 isso tem que ser = y (y ln x - 1).
isso tem que ser = y (y ln x - 1).



 , avisa que eu resolvo.
, avisa que eu resolvo.

