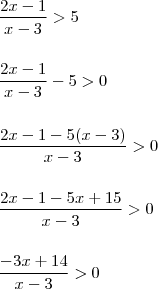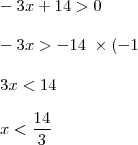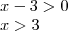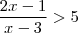
Dúvida: Por que o denominador não tem o seu sinal alterado quando a equação é multiplicada por menos um?
Minha Resolução:



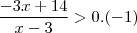

Obs: O restante da resolução eu conseguir concluir, que inclusive é S = {
 } e realmente concorda com a do livro [Um curso de Cálculo, Volume 1, Hamilton Luiz Guidorizzi] de onde foi retirada a questão, no entanto a única forma de chegar a mesma foi com o denominador sendo "x-3", o que não concordo, pois para mim, após multiplicar por menos um, deveria ficar "x+3".
} e realmente concorda com a do livro [Um curso de Cálculo, Volume 1, Hamilton Luiz Guidorizzi] de onde foi retirada a questão, no entanto a única forma de chegar a mesma foi com o denominador sendo "x-3", o que não concordo, pois para mim, após multiplicar por menos um, deveria ficar "x+3".Assim, volto ao questionamento: Porque o denominador não tem o seu sinal alterado quando a equação é multiplicada por menos um?