Não consigo concluir esse exercício:
Se o polinômio x3+kx2-2x+3 é divisível pelo polinômio x2-x+1, qual é o quociente?
Já tentei pelo método da chave, mas ao verificar o resto não é coerente com as respostas propostas...



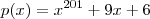 e
e 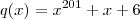 Temos 9 \neq 1 , logo p \neq q ..
Temos 9 \neq 1 , logo p \neq q ..
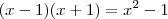 .
.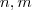 em
em  ,definamos
,definamos 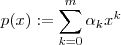 e
e 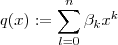 com
com 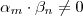 .
.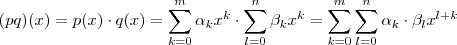 , como o maior valor que
, como o maior valor que 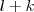 assume é
assume é  o resultado segue .
o resultado segue . 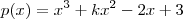 e
e 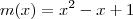 .
. 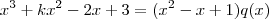 . Como o polinômio no 1° membro e de grau 3 , pelo lemma 2 concluímos que o polinômio q é de grau 1 , i.e,
. Como o polinômio no 1° membro e de grau 3 , pelo lemma 2 concluímos que o polinômio q é de grau 1 , i.e, 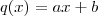 (a,b a serem determinados )
(a,b a serem determinados ) 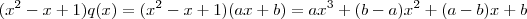 . Assim , pelo Lemma 1 , temos que
. Assim , pelo Lemma 1 , temos que 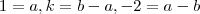 e
e 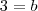 e portanto
e portanto 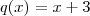 .
.
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes

 .
.
 :
: