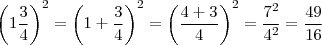por aynee » Sex Jul 18, 2014 12:37
por aynee » Sex Jul 18, 2014 12:37
Estou em duvida, não chego ao resultado, alguém pode me ajudar?
(1 3/4) elevado a 2 é uma fração mista. Att
-
aynee
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Sex Jul 18, 2014 12:29
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por Russman » Sex Jul 18, 2014 13:15
por Russman » Sex Jul 18, 2014 13:15
É simples. Uma fração do tipo
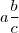
quer significar
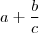
que é, na realidade,

.
Assim, se você tem que simplificar

, então há duas forma de fazer. A primeira é lembrar que
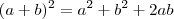
Daí,

.
Ou, então
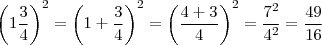
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
 por aynee » Sex Jul 18, 2014 18:35
por aynee » Sex Jul 18, 2014 18:35
Nossa, agora ficou mais claro, obrigado
-
aynee
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Sex Jul 18, 2014 12:29
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
Voltar para Álgebra Elementar
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- duvida sobre inverso mod m de matriz
por gwirith » Dom Mai 17, 2009 21:11
- 0 Respostas
- 1961 Exibições
- Última mensagem por gwirith

Dom Mai 17, 2009 21:11
Matrizes e Determinantes
-
- (ITA-SP) Elementos da diagonal principal do inverso
por Carolziiinhaaah » Qua Jun 23, 2010 18:15
- 2 Respostas
- 7968 Exibições
- Última mensagem por Carolziiinhaaah

Qua Jun 23, 2010 19:42
Matrizes e Determinantes
-
- [Série de potÊncia] Expansão de séries de potência
 por Adonias 7 » Qua Jun 01, 2016 09:05
por Adonias 7 » Qua Jun 01, 2016 09:05
- 0 Respostas
- 3686 Exibições
- Última mensagem por Adonias 7

Qua Jun 01, 2016 09:05
Sequências
-
- Tópico de análise: determinação de campo de quadrado inverso
por ant_dii » Qui Dez 01, 2011 03:10
- 4 Respostas
- 2447 Exibições
- Última mensagem por ant_dii

Sáb Dez 03, 2011 11:39
Cálculo: Limites, Derivadas e Integrais
-
- [Função Inversa] Dúvida sobre como calcular a inverso
por Richard Oliveira » Sex Nov 04, 2011 16:36
- 3 Respostas
- 4441 Exibições
- Última mensagem por Richard Oliveira

Sáb Nov 05, 2011 02:54
Funções
Usuários navegando neste fórum: Nenhum usuário registrado e 3 visitantes
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 12:41
pessoal eu achei como resultado 180 toneladas,entretanto sei que a questão está erra pela lógica e a resposta correta segundo o gabarito é 1.800 toneladas.
me explique onde eu estou pecando na questão. resolva explicando.
78 – ( CEFET – 1993 ) Os desabamentos, em sua maioria, são causados por grande acúmulo de lixo nas encostas dos morros. Se 10 pessoas retiram 135 toneladas de lixo em 9 dias, quantas toneladas serão retiradas por 40 pessoas em 30 dias ?
Assunto:
dúvida em uma questão em regra de 3!
Autor:
Douglasm - Qui Jul 01, 2010 13:16
Observe o raciocínio:
10 pessoas - 9 dias - 135 toneladas
1 pessoa - 9 dias - 13,5 toneladas
1 pessoa - 1 dia - 1,5 toneladas
40 pessoas - 1 dia - 60 toneladas
40 pessoas - 30 dias - 1800 toneladas
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:18
pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:21
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
valeu meu camarada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



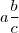 quer significar
quer significar 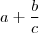 que é, na realidade,
que é, na realidade,  .
. , então há duas forma de fazer. A primeira é lembrar que
, então há duas forma de fazer. A primeira é lembrar que 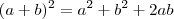
 .
.