Tentar resolver os seguintes exercícios
1)Um carro, viajando à velocidade média de 80 km/h, gasta três horas para percorrer um trecho entre duas cidades.
Quanto tempo esse carro levaria para percorrer o mesmo trecho, se a velocidade média fosse 20% menor?
a) 3h30min
b) 3h45min
c) 4h00min
d) 4h15min
e) 4h30min
2 - No fim do ano, os empregados de um estacionamento fizeram uma “caixinha de Natal” e combinaram que o valor
arrecadado seria dividido igualmente entre eles. Conseguiram um total de R$ 540,00 e dividiram pelo número de
atendentes, para saber a quantia que caberia a cada um. Mas tinham esquecido de incluir na partilha os 2 vigias
noturnos, de modo que fizeram nova divisão, pela qual coube a cada um R$ 9,00 a menos do que na divisão anterior.
No final, cada um recebeu:
a) R$ 42,00.
b) R$ 45,00.
c) R$ 48,00.
d) R$ 50,00.
e) R$ 52,00.



 . Por outro lado,
. Por outro lado, 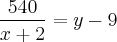 . Daí, vem que:
. Daí, vem que:  e
e 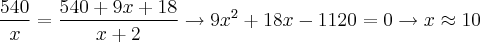 . Assim,
. Assim,  .
. em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.