Eu vi a resolução deste exercício e cheguei a conclusão de que eu realmente não conseguiria terminar, pois não sei da onde veio a última propriedade:
(FUVEST) O triângulo ABC está inscrito numa circunferência de raio 5 cm. Sabe-se que A e B são extremidades de um diâmetro e que a corda BC mede 6 cm. Então a área do triângulo ABC, em cm², vale:
a)24
b)12
c)5V3/2
d)6V2
e)2V3
Resolução:
AB = 10
BC = 6
AC² + BC² = AB² ----> AC² + 6² = (5 + 5)² ----> AC = 8
Da onde, da onde veio isso?? > S = BC*AC/2 -----> S = 6*8/2 -----> S = 24


 qualquer circulo centrado em
qualquer circulo centrado em  . Seja,
. Seja,  três pontos distintos , tais que
três pontos distintos , tais que  .(Note que M é ponto médio de BD) . Note que ,
.(Note que M é ponto médio de BD) . Note que , 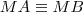 e
e  . Logo , os triângulos
. Logo , os triângulos 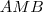 e
e 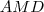 são isósceles e com isso
são isósceles e com isso 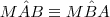 e
e 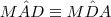 (*) .
(*) .  e
e  são suplementares ,então
são suplementares ,então 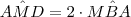 .Usando que a soma dos ângulos internos de qualquer triângulo vale 2 ângulos retos + a informação (*) , tem-se que
.Usando que a soma dos ângulos internos de qualquer triângulo vale 2 ângulos retos + a informação (*) , tem-se que 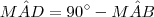 o que prova que
o que prova que 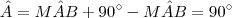 .
.
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
 e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)