Esboce o gráfico de f (x) = x|x|. Para que valores de x, f é diferenciável? Encontre uma fórmula para f ' .
Alguém ajuda?



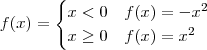



young_jedi escreveu:podemos dizer o seguinte
esta função é diferenciavel em qualquer ponto da mesma, pois é uma função continua
uma formula para a derivada seria derivar a função em cada uma das condições


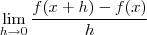
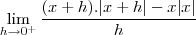
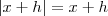
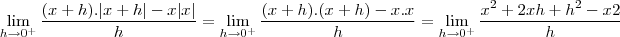

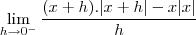

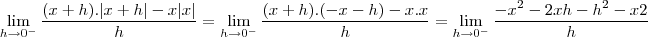
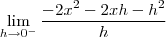


Voltar para Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante


 , avisa que eu resolvo.
, avisa que eu resolvo.

