Estou tentando resolver esse exercício de produto vetorial, mas não consigo encontrar a resposta do gabarito, sei que se são ortogonais, o produto entre eles é 0, mas não to sabendo como resolver essa questão.
Questão- Ache u tal que ||u||=3
![\sqrt[]{}](/latexrender/pictures/fe30ef6b9007d97ba11036078c300fe0.png "\sqrt[]{}")
3 e u é ortogonal a v=(2,-3,-1) e a w=(2,-4,6). Dos u encontrados, qual forma ângulo com o vetor (1,0,0).OBS(u,v e w, são vetores)
Gabarito:u=(3,-3,-3)
Desde já agradeço a resposta! =)
e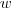 
nos fornecerá um outro vetor o qual é simultaneamente ortogonal aos vetores 
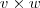(produto vetorial entre v e w ) , o que significa que existe algum n° real 
para o qual 
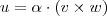. Para encontrar um dos escalares (são dois , e são simétricos ) , basta utilizar que a norma de 
vale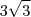 
juntamente com a segunda hipótese .
por 
.
