Lembre-se que a
velocidade média 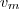
desenvolvida pelo móvel no intervalo de tempo
![[t_1,t_2] [t_1,t_2]](/latexrender/pictures/7460d8dce724ee4546f591b3f1b795b4.png)
é definida como
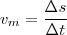
onde
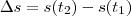
é o deslocamento sofrido e
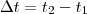
.
Assim, por exemplo, para calcular a velocidade média desenvolvida no intervalo
![[3,4] [3,4]](/latexrender/pictures/b814fa889082069ffb727ee1623c0944.png)
basta substituir, já que é conhecida, os valores de tempo na função deslocamento. Veja,


Não se engane com o sinal negativo. Ele e o sinal positivo apenas indicam o
sentido do movimento. Se a posição cresce para a direita(como usualmente se faz) e a velocidade média desenvolvida no intervalo de tempo de interesse tem sinal negativo, então o móvel se desloca no sentido de decrescimento da posição nesse intervalo de tempo. Ou seja, para a esquerda.
A
velocidade instantânea 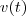
é calculada para um instante de tempo específico através do limite
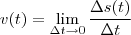
que , na prática, é a derivada com relação a

da função posição. Isto é,

.
Portanto,
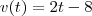
e basta substituir

pelo instante que se deseja calcular a velocidade instantânea.
No conhecimento desta, é útil saber(e simples de mostrar) que a velocidade média desenvolvida no intervalo
![[t_1,t_2] [t_1,t_2]](/latexrender/pictures/7460d8dce724ee4546f591b3f1b795b4.png)
se relaciona com a velocidade instantânea nos instantes

e

por
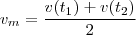
.
Ou seja, a velocidade média desenvolvida no intervalo de tempo de interesse é a média aritmética simples das velocidades instantâneas desenvolvidas nos extremos desse intervalo.


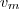 desenvolvida pelo móvel no intervalo de tempo
desenvolvida pelo móvel no intervalo de tempo ![[t_1,t_2] [t_1,t_2]](/latexrender/pictures/7460d8dce724ee4546f591b3f1b795b4.png) é definida como
é definida como 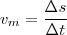
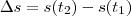 é o deslocamento sofrido e
é o deslocamento sofrido e 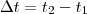 .
.![[3,4] [3,4]](/latexrender/pictures/b814fa889082069ffb727ee1623c0944.png) basta substituir, já que é conhecida, os valores de tempo na função deslocamento. Veja,
basta substituir, já que é conhecida, os valores de tempo na função deslocamento. Veja,

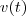 é calculada para um instante de tempo específico através do limite
é calculada para um instante de tempo específico através do limite 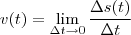
 da função posição. Isto é,
da função posição. Isto é,  .
.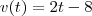 e basta substituir
e basta substituir  e
e  por
por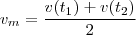 .
.
