


 .
.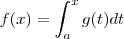 (a constante ) . Segue-se
(a constante ) . Segue-se 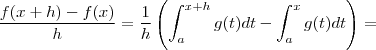
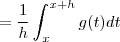 .
.  , a integral de
, a integral de  sobre o intervalo
sobre o intervalo ![[x,x+h] [x,x+h]](/latexrender/pictures/11f83f7cd0c0bd01081e20010153ffe9.png) pode ser aproximada por
pode ser aproximada por 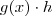 e com isso
e com isso  .Alternativamente ,deixe
.Alternativamente ,deixe  ser um intervalo fechado de extremos x, x+h .Temos que
ser um intervalo fechado de extremos x, x+h .Temos que 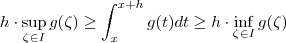 sse
sse 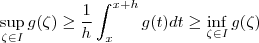 .
. 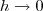 , tem-se que
, tem-se que  e portanto
e portanto  .
. ![[f(p(x))]' = f'(p(x)) \cdot p'(x) = g(p(x))p'(x) [f(p(x))]' = f'(p(x)) \cdot p'(x) = g(p(x))p'(x)](/latexrender/pictures/528d75a29676646907628f08b99f920a.png) . Agora vamos obter a fórmula destacada .Para tal ,fixe x e suponha
. Agora vamos obter a fórmula destacada .Para tal ,fixe x e suponha  (o caso q(x) = p(x) é trivial) . Neste caso , existe
(o caso q(x) = p(x) é trivial) . Neste caso , existe  entre
entre  e
e  .(O intervalo não é degenerado) e assim
.(O intervalo não é degenerado) e assim  . Daí, ao derivarmos com respeito à x e utilizando os resultados obtidos teremos a fórmula destacada .
. Daí, ao derivarmos com respeito à x e utilizando os resultados obtidos teremos a fórmula destacada .
Voltar para Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 3 visitantes