 por amigao » Ter Jul 01, 2014 20:23
por amigao » Ter Jul 01, 2014 20:23
Estou resolvendo um exercicio de sistemas de equações diferenciais e encontrei os autovalores, mas estou com problemas para encontrar os autovetores para quando o lambda é complexo.
tenho que resolver isso:
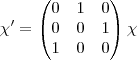
Dai meu auto valores são:

= 1
![\lambda = -1+ \sqrt[]{3} i \lambda = -1+ \sqrt[]{3} i](/latexrender/pictures/6de4c91707eff52ea4ad3cf3a5909045.png)
![\lambda = -1- \sqrt[]{3} i \lambda = -1- \sqrt[]{3} i](/latexrender/pictures/60f4b1dba4dfab5b3de48e800d388ef8.png)
Quando escolho o
![\lambda = -1+ \sqrt[]{3} i \lambda = -1+ \sqrt[]{3} i](/latexrender/pictures/6de4c91707eff52ea4ad3cf3a5909045.png)
e tento achar os autovetores eu fico com o tal sistema
![(-1+ \sqrt[]{3} i)v1=-v2 \\
(-1+ \sqrt[]{3} i)v2=-v3 \\
(-1+ \sqrt[]{3} i)v3=-v1 \\ (-1+ \sqrt[]{3} i)v1=-v2 \\
(-1+ \sqrt[]{3} i)v2=-v3 \\
(-1+ \sqrt[]{3} i)v3=-v1 \\](/latexrender/pictures/16cd0eb9fbf809e8c34d1c1c20bbb482.png)
e não consigo escolher quais v1, v2 e v3 diferente de 0,0,0 que satisfaça o sistema para montar um autovetor.
Me ajudem por favor, urgente!!
grato
-
amigao
- Usuário Dedicado

-
- Mensagens: 28
- Registrado em: Sáb Mai 11, 2013 11:52
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: cursando
 por Russman » Qua Jul 02, 2014 00:14
por Russman » Qua Jul 02, 2014 00:14
Primeiramente, eu acredito que você tenha esquecido de dividir os autovalores complexos por 2.
O(s) sistema(s) que você obterá serão da forma

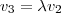

Assim, já que

, a solução é



onde

.
Ou seja, o conjunto de autovetores da matriz para o autovalor

são os múltiplos reais de
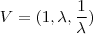
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
 por amigao » Qua Jul 02, 2014 14:45
por amigao » Qua Jul 02, 2014 14:45
Russman escreveu:Primeiramente, eu acredito que você tenha esquecido de dividir os autovalores complexos por 2.
O(s) sistema(s) que você obterá serão da forma

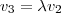

Assim, já que

, a solução é



onde

.
Ou seja, o conjunto de autovetores da matriz para o autovalor

são os múltiplos reais de
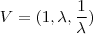
Nossa verdade, bem lembrado!!
Muito obrigado ajudou muito.
-
amigao
- Usuário Dedicado

-
- Mensagens: 28
- Registrado em: Sáb Mai 11, 2013 11:52
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: cursando
Voltar para Álgebra Linear
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [autovalores/autovetores] Encontrar autovetores e autovalore
por amigao » Sáb Nov 23, 2013 15:42
- 1 Respostas
- 1988 Exibições
- Última mensagem por e8group

Sáb Nov 23, 2013 19:13
Álgebra Linear
-
- Autovetores
por baianinha » Sáb Ago 06, 2011 12:07
- 3 Respostas
- 2250 Exibições
- Última mensagem por MarceloFantini

Sáb Ago 06, 2011 22:50
Matrizes e Determinantes
-
- autovalores e autovetores
por natan matos » Ter Nov 30, 2010 23:05
- 0 Respostas
- 1894 Exibições
- Última mensagem por natan matos

Ter Nov 30, 2010 23:05
Matrizes e Determinantes
-
- Álgebra Linear II - Autovalores e Autovetores
por Cleyson007 » Qua Nov 09, 2011 08:56
- 1 Respostas
- 2158 Exibições
- Última mensagem por MarceloFantini

Qua Nov 09, 2011 17:33
Álgebra Linear
-
- [Algebra Linear] autovalores e autovetores
por Angel31 » Sex Out 26, 2012 10:25
- 3 Respostas
- 3011 Exibições
- Última mensagem por MarceloFantini

Sáb Out 27, 2012 08:17
Álgebra Linear
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
Unesp - 95 Números Complexos
Autor:
Alucard014 - Dom Ago 01, 2010 18:22
(UNESP - 95) Seja L o Afixo de um Número complexo

em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
Assunto:
Unesp - 95 Números Complexos
Autor:
MarceloFantini - Qui Ago 05, 2010 17:27
Seja

o ângulo entre o eixo horizontal e o afixo

. O triângulo é retângulo com catetos

e

, tal que

. Seja

o ângulo complementar. Então

. Como

, o ângulo que o afixo

formará com a horizontal será

, mas negativo pois tem de ser no quarto quadrante. Se

, então

. Como módulo é um:

.
Logo, o afixo é

.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
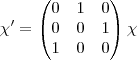
 = 1
= 1![\lambda = -1+ \sqrt[]{3} i \lambda = -1+ \sqrt[]{3} i](/latexrender/pictures/6de4c91707eff52ea4ad3cf3a5909045.png)
![\lambda = -1- \sqrt[]{3} i \lambda = -1- \sqrt[]{3} i](/latexrender/pictures/60f4b1dba4dfab5b3de48e800d388ef8.png)
![\lambda = -1+ \sqrt[]{3} i \lambda = -1+ \sqrt[]{3} i](/latexrender/pictures/6de4c91707eff52ea4ad3cf3a5909045.png) e tento achar os autovetores eu fico com o tal sistema
e tento achar os autovetores eu fico com o tal sistema![(-1+ \sqrt[]{3} i)v1=-v2 \\
(-1+ \sqrt[]{3} i)v2=-v3 \\
(-1+ \sqrt[]{3} i)v3=-v1 \\ (-1+ \sqrt[]{3} i)v1=-v2 \\
(-1+ \sqrt[]{3} i)v2=-v3 \\
(-1+ \sqrt[]{3} i)v3=-v1 \\](/latexrender/pictures/16cd0eb9fbf809e8c34d1c1c20bbb482.png)



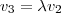

 , a solução é
, a solução é


 .
.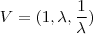

 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.