Alguém poderia me ajudar na questão de funções da UFJF 2009?
É a questão 11 desta prova:
http://siga.ufjf.br/index.php?module=ve ... va1a_2.pdf
Aguardo respostas, obrigada!



 e
e  são obtidos a partir da intersecção do gráfico
são obtidos a partir da intersecção do gráfico  com
com 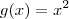 , vamos obter as ordenadas substituindo em
, vamos obter as ordenadas substituindo em  .
. 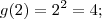 e
e  . Logo, tem-se:
. Logo, tem-se:
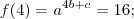
 dos dois lados (uma vez que
dos dois lados (uma vez que  e
e 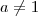 pelo enunciado), temos:
pelo enunciado), temos:

 . Logo:
. Logo: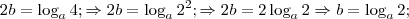
 .
.

Maira escreveu:Alguém poderia me ajudar na questão de funções da UFJF 2009?
É a questão 11 desta prova:
http://siga.ufjf.br/index.php?module=ve ... va1a_2.pdf
Aguardo respostas, obrigada!
 e
e  os gráficos se cruzam.
os gráficos se cruzam. e
e  . Mas
. Mas 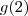 e
e 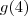 é fácil de achar:
é fácil de achar:

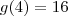
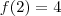 e
e 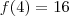 . Vamos usar este resultado agora:
. Vamos usar este resultado agora: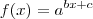
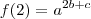
 (equação 1)
(equação 1)
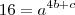 (equação 2)
(equação 2)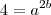

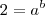
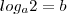



Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes

 .
.
 :
: