 por natanaelskt » Dom Jun 29, 2014 13:02
por natanaelskt » Dom Jun 29, 2014 13:02
Estou com dúvida neste exercício,na verdade nem sei como começar a fazer. me ajudem ai galera. postei o exercício em anexo. mas já to começando a aprender o látex. mas minhas provas tá perto,por isso to postando até ficar bom no látex.
tem um outro parecido com este que também não sei como começar a fazer. irei postar este também. alguém poderia me indicar um livro que tem exercícios resolvidos de cálculo I? eu precisava de um livro com exercícios difíceis resolvidos. eu acho tenho listas com exercícios daora para a prova,mas estão sem respostas. e não consigo fazer a maioria,por isso to postando aqui.
- Anexos
-
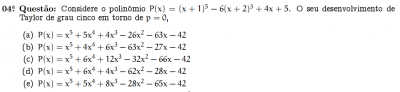
-
natanaelskt
- Usuário Dedicado

-
- Mensagens: 32
- Registrado em: Seg Mar 11, 2013 15:06
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por e8group » Dom Jun 29, 2014 14:21
por e8group » Dom Jun 29, 2014 14:21
Segue direto da definição (tome f(x) = polinômio dado ) .Então ,
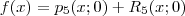
.Onde :
^k}{k!} p_5(x;0) = \sum_{k=0}^5 \frac{D^k [f (0)](x-0)^k}{k!}](/latexrender/pictures/cb34c16138db6fb1cc52543c3a2ce77c.png)
e
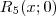
pode ser computado de diversas formas (conheço duas : Forma Lagrange e Forma Cauchy , pode google p/ ver )
Exemplo :
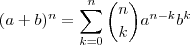
(Teorema binomial )
Dem. (Usando Taylor polinômio + erro associado pela forma Lagrange)
Defina
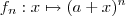
. (
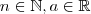
)
Podemos escrever (vide def. livros de análise numérica )
![f_n(x) = \sum_{k=0}^{n} \frac{D^k[f_n(0)] (x-0)^k}{k!} + R_n(x;0) = f_n(x) = \sum_{k=0}^{n} \frac{D^k[f_n(0)] (x-0)^k}{k!} + R_n(x;0) =](/latexrender/pictures/a1ba734966359352e7e3eee4456c5006.png)
.
Note que
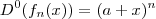
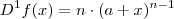
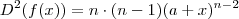
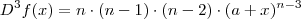
(...)
Expressão geral : (k= 0 ,1,2,3,...,n) :
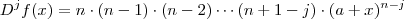
Mas ,
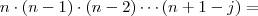
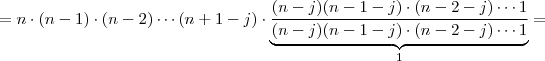
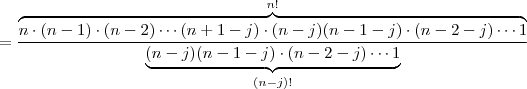
Logo ,
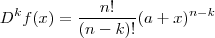
o que implica que
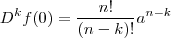
.
Assim , obtemos
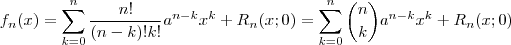
.
Mas, qualquer derivada de ordem superiores ao grau

do polinômio relativo ao mesmo é constante igual a zero , então pela forma de Lagrange temos
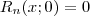
e o resultado segue .
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por natanaelskt » Qua Jul 02, 2014 02:08
por natanaelskt » Qua Jul 02, 2014 02:08
Obrigado,santhiago!
-
natanaelskt
- Usuário Dedicado

-
- Mensagens: 32
- Registrado em: Seg Mar 11, 2013 15:06
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [polinômio de taylor] - Dúvida sobre o exercício
 por natanaelskt » Ter Jul 08, 2014 11:41
por natanaelskt » Ter Jul 08, 2014 11:41
- 0 Respostas
- 1725 Exibições
- Última mensagem por natanaelskt

Ter Jul 08, 2014 11:41
Cálculo: Limites, Derivadas e Integrais
-
- Polinomio de taylor - Dúvida sobre o erro.
por natanaelskt » Seg Jun 23, 2014 18:55
- 0 Respostas
- 1673 Exibições
- Última mensagem por natanaelskt

Seg Jun 23, 2014 18:55
Cálculo: Limites, Derivadas e Integrais
-
- polinomio de taylor
por ezidia51 » Ter Set 24, 2019 00:09
- 6 Respostas
- 6044 Exibições
- Última mensagem por ezidia51

Qua Set 25, 2019 23:49
Cálculo: Limites, Derivadas e Integrais
-
- [Calculo 1] Polinômio de Taylor
por LuisLemos » Seg Ago 01, 2016 22:36
- 1 Respostas
- 3417 Exibições
- Última mensagem por Cleyson007

Ter Ago 02, 2016 12:40
Cálculo: Limites, Derivadas e Integrais
-
- Polinômio de Taylor de ordem 2
por Maisa_Rany » Seg Nov 19, 2018 16:53
- 2 Respostas
- 8117 Exibições
- Última mensagem por Maisa_Rany

Ter Nov 20, 2018 16:26
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 6 visitantes
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 12:41
pessoal eu achei como resultado 180 toneladas,entretanto sei que a questão está erra pela lógica e a resposta correta segundo o gabarito é 1.800 toneladas.
me explique onde eu estou pecando na questão. resolva explicando.
78 – ( CEFET – 1993 ) Os desabamentos, em sua maioria, são causados por grande acúmulo de lixo nas encostas dos morros. Se 10 pessoas retiram 135 toneladas de lixo em 9 dias, quantas toneladas serão retiradas por 40 pessoas em 30 dias ?
Assunto:
dúvida em uma questão em regra de 3!
Autor:
Douglasm - Qui Jul 01, 2010 13:16
Observe o raciocínio:
10 pessoas - 9 dias - 135 toneladas
1 pessoa - 9 dias - 13,5 toneladas
1 pessoa - 1 dia - 1,5 toneladas
40 pessoas - 1 dia - 60 toneladas
40 pessoas - 30 dias - 1800 toneladas
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:18
pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:21
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
valeu meu camarada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


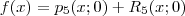 .Onde :
.Onde : ^k}{k!} p_5(x;0) = \sum_{k=0}^5 \frac{D^k [f (0)](x-0)^k}{k!}](/latexrender/pictures/cb34c16138db6fb1cc52543c3a2ce77c.png) e
e 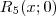 pode ser computado de diversas formas (conheço duas : Forma Lagrange e Forma Cauchy , pode google p/ ver )
pode ser computado de diversas formas (conheço duas : Forma Lagrange e Forma Cauchy , pode google p/ ver )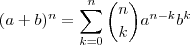 (Teorema binomial )
(Teorema binomial ) 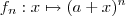 . (
. (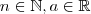 )
) ![f_n(x) = \sum_{k=0}^{n} \frac{D^k[f_n(0)] (x-0)^k}{k!} + R_n(x;0) = f_n(x) = \sum_{k=0}^{n} \frac{D^k[f_n(0)] (x-0)^k}{k!} + R_n(x;0) =](/latexrender/pictures/a1ba734966359352e7e3eee4456c5006.png) .
.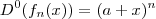
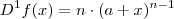
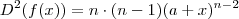
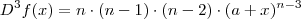
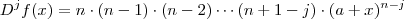
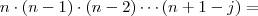
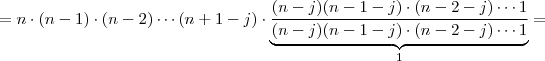
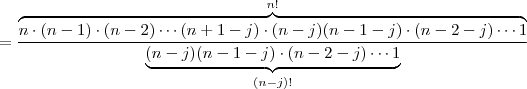
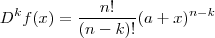 o que implica que
o que implica que 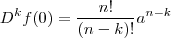 .
. 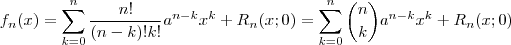 .
.  do polinômio relativo ao mesmo é constante igual a zero , então pela forma de Lagrange temos
do polinômio relativo ao mesmo é constante igual a zero , então pela forma de Lagrange temos 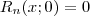 e o resultado segue .
e o resultado segue .