 por ulisses123 » Sex Jun 20, 2014 15:42
por ulisses123 » Sex Jun 20, 2014 15:42
O gráfico de uma função g tem por assímptotas x =2 e y =5
Então o gráfico da função f , definida por f (x) =g(x +1)´- 2 tem por
assímptotas:
-
ulisses123
- Usuário Dedicado

-
- Mensagens: 30
- Registrado em: Sex Jun 20, 2014 14:48
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: curso tecnico em gestao
- Andamento: formado
 por e8group » Sex Jun 20, 2014 19:10
por e8group » Sex Jun 20, 2014 19:10
O que está acontecendo é a translação horizontal e vertical do gráfico .
Se
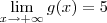
; formalmente isso significa que para cada

que propormos existe um número

correspondente ( ">>" para enfatizar que em geral ele está mt longe da origem) tal que se
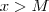
então a função

avaliada em

fica muito próximo de

(
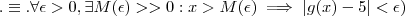
.
Nota-se que a porção do gráfico de g ( x > M) está dentro da caixa de altura
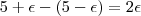
e base 'infinita' (
![\{(x,g(x) ; x > M \} \subset [M,+\infty) \times [5-\epsilon , 5+\epsilon ] \{(x,g(x) ; x > M \} \subset [M,+\infty) \times [5-\epsilon , 5+\epsilon ]](/latexrender/pictures/ef9574ad537c80b89d95f4a98c02ef4a.png)
) .
Se agente transladar o gráfico de g , façamos o mesmo com caixa de forma conveniente , e o seu novo gráfico continuará dentro da caixa .De fato ,
Se
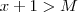
então
![| [g(x+1) -2] -3 | = |g(x+1) - 5 | < \epsilon | [g(x+1) -2] -3 | = |g(x+1) - 5 | < \epsilon](/latexrender/pictures/71173129b0bca055ee8700f4aa745eaf.png)
, ou seja ,
se
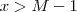
então
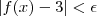
, logo a porção do gráfico de

x > M-1 está dentro da caixa de altura mesma da caixa anterior e também base infinita (
![\{(x,f(x)) ; x > M - 1\} \subset [M-1,+\infty) \times [4-\epsilon , 4+\epsilon ] \{(x,f(x)) ; x > M - 1\} \subset [M-1,+\infty) \times [4-\epsilon , 4+\epsilon ]](/latexrender/pictures/3c7b8d34c07af78d3182ab95bebd5b17.png)
)e muito mais que isso estamos dizendo formalmente que
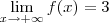
.
De forma prática ,
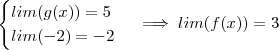
.
Tente fazer o outro .
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
Voltar para Funções
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Funções reais. como resolver estas funções...
por LEANDRO HENRIQUE » Ter Mar 04, 2014 18:43
- 0 Respostas
- 3424 Exibições
- Última mensagem por LEANDRO HENRIQUE

Ter Mar 04, 2014 18:43
Funções
-
- [Funções] Domínio e a imagem de funções
 por concurseironf » Qui Ago 21, 2014 12:24
por concurseironf » Qui Ago 21, 2014 12:24
- 1 Respostas
- 4192 Exibições
- Última mensagem por Pessoa Estranha

Sex Ago 22, 2014 20:11
Funções
-
- [Funções] questões de funções
por Zandrojr » Qua Ago 31, 2011 11:39
- 0 Respostas
- 3137 Exibições
- Última mensagem por Zandrojr

Qua Ago 31, 2011 11:39
Funções
-
- Funções
por Revelants » Dom Out 05, 2008 15:07
- 1 Respostas
- 3387 Exibições
- Última mensagem por Molina

Dom Out 05, 2008 15:53
Cálculo: Limites, Derivadas e Integrais
-
- Funçoes
por Luna » Seg Set 28, 2009 20:02
- 1 Respostas
- 2994 Exibições
- Última mensagem por Marcampucio

Seg Set 28, 2009 21:35
Funções
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 12:41
pessoal eu achei como resultado 180 toneladas,entretanto sei que a questão está erra pela lógica e a resposta correta segundo o gabarito é 1.800 toneladas.
me explique onde eu estou pecando na questão. resolva explicando.
78 – ( CEFET – 1993 ) Os desabamentos, em sua maioria, são causados por grande acúmulo de lixo nas encostas dos morros. Se 10 pessoas retiram 135 toneladas de lixo em 9 dias, quantas toneladas serão retiradas por 40 pessoas em 30 dias ?
Assunto:
dúvida em uma questão em regra de 3!
Autor:
Douglasm - Qui Jul 01, 2010 13:16
Observe o raciocínio:
10 pessoas - 9 dias - 135 toneladas
1 pessoa - 9 dias - 13,5 toneladas
1 pessoa - 1 dia - 1,5 toneladas
40 pessoas - 1 dia - 60 toneladas
40 pessoas - 30 dias - 1800 toneladas
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:18
pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:21
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
valeu meu camarada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



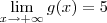 ; formalmente isso significa que para cada
; formalmente isso significa que para cada  que propormos existe um número
que propormos existe um número  correspondente ( ">>" para enfatizar que em geral ele está mt longe da origem) tal que se
correspondente ( ">>" para enfatizar que em geral ele está mt longe da origem) tal que se 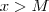 então a função
então a função  avaliada em
avaliada em  fica muito próximo de
fica muito próximo de  (
(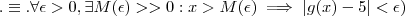 .
.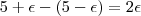 e base 'infinita' (
e base 'infinita' ( ![\{(x,g(x) ; x > M \} \subset [M,+\infty) \times [5-\epsilon , 5+\epsilon ] \{(x,g(x) ; x > M \} \subset [M,+\infty) \times [5-\epsilon , 5+\epsilon ]](/latexrender/pictures/ef9574ad537c80b89d95f4a98c02ef4a.png) ) .
) . 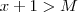 então
então ![| [g(x+1) -2] -3 | = |g(x+1) - 5 | < \epsilon | [g(x+1) -2] -3 | = |g(x+1) - 5 | < \epsilon](/latexrender/pictures/71173129b0bca055ee8700f4aa745eaf.png) , ou seja ,
, ou seja , 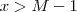 então
então 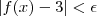 , logo a porção do gráfico de
, logo a porção do gráfico de  x > M-1 está dentro da caixa de altura mesma da caixa anterior e também base infinita (
x > M-1 está dentro da caixa de altura mesma da caixa anterior e também base infinita (![\{(x,f(x)) ; x > M - 1\} \subset [M-1,+\infty) \times [4-\epsilon , 4+\epsilon ] \{(x,f(x)) ; x > M - 1\} \subset [M-1,+\infty) \times [4-\epsilon , 4+\epsilon ]](/latexrender/pictures/3c7b8d34c07af78d3182ab95bebd5b17.png) )e muito mais que isso estamos dizendo formalmente que
)e muito mais que isso estamos dizendo formalmente que 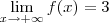 .
.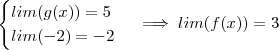 .
. 