No intervalo
 , o valor médio de f(t),
, o valor médio de f(t), 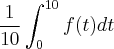 é:
é:a) entre 0 e 1;
b) 0;
c) entre 0 e -1;
d) g(1);
e) entre -1 e -2.
Não sei como responder.

 , o valor médio de f(t),
, o valor médio de f(t), 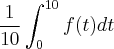 é:
é:
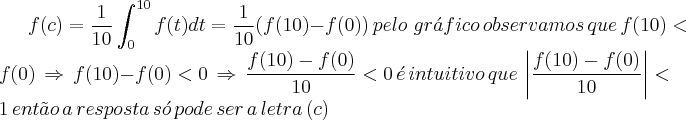

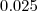 (levando em conta que o raciocínio estar certo ) . Infelizmente perdi a conexão com a internet e o que eu tinha feito perdi .
(levando em conta que o raciocínio estar certo ) . Infelizmente perdi a conexão com a internet e o que eu tinha feito perdi . ![[0,1] ; [1,3] ; [3,7] ; [7,9] [0,1] ; [1,3] ; [3,7] ; [7,9]](/latexrender/pictures/a1399b15beac5a65e106b28407e3e8c8.png) e
e ![[9,10] [9,10]](/latexrender/pictures/161d392c82c6c3fa93f611bd9284b6b6.png) .
. 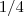 é menor que a integral de f(x) sobre o mesmo intervalo ; no segundo (compare por área de retângulo ) ,
é menor que a integral de f(x) sobre o mesmo intervalo ; no segundo (compare por área de retângulo ) , 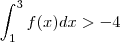 ; no terceiro (compare por área de trapézio ) ,
; no terceiro (compare por área de trapézio ) ,  ; no quarto (compare por área de retângulo )
; no quarto (compare por área de retângulo ) 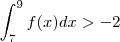 e no último (compare com área de triângulo )
e no último (compare com área de triângulo )  .
. 



 . Nós temos
. Nós temos 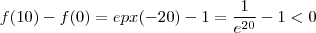 , mas !
, mas ! 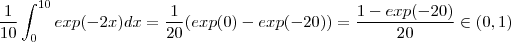 .
.  , pois vê-se no gráfico que a função é limitada inferiormente por
, pois vê-se no gráfico que a função é limitada inferiormente por  e superiormente por
e superiormente por  e a integral cumpre com a monotonicidade .
e a integral cumpre com a monotonicidade .  e
e 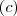 entretanto , pelo post acima visto que a integral é limitada inferiormente por um n° entre zero e 1 ; logo só pode ser (a) .
entretanto , pelo post acima visto que a integral é limitada inferiormente por um n° entre zero e 1 ; logo só pode ser (a) . 

Voltar para Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)
zig escreveu:

 , ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio. ![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
 da seguinte forma:
da seguinte forma: .
. da seguinte forma:
da seguinte forma: .
.