 por leticiapires52 » Ter Jun 17, 2014 10:55
por leticiapires52 » Ter Jun 17, 2014 10:55
A indução matemática é uma ferramenta que permite estabelecer verdades matemáticas válidas sobre subconjuntos infinitos de números naturais, isto é, trata de provar que uma sentença aberta é verdadeira para um certo, então para verificar se o princípio é valido o que deve ser feito?
-
leticiapires52
- Colaborador Voluntário

-
- Mensagens: 100
- Registrado em: Qua Fev 12, 2014 10:12
- Formação Escolar: GRADUAÇÃO
- Área/Curso: licenciatura em matemática
- Andamento: cursando
 por e8group » Qui Jun 19, 2014 14:19
por e8group » Qui Jun 19, 2014 14:19
A ideia é ... dada uma propriedade
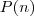
a qual é verdadeira para

,você supõe que para um

arbitrário
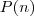
é verdadeira e com base nesta suposição mostra que
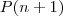
também é verdadeira . Ou seja, você está dizendo que
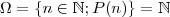
, pois
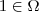
e
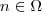
(Hipótese )
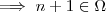
implicando
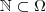
.(Se o todo é sempre maior que qualquer uma de suas partes e esta é maior o todo ; logo só pode ser
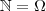
)
Para começar a brincadeira ...comece com

= o subconjunto dos números naturais

para os quais
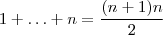
,i.e,
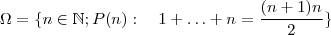
.
Deve-se fazer o seguinte :
(i) Verificar que

pertence a

,i.e , checkar se
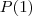
é verdadeiro .
(ii) Sendo
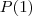
verdadeiro ; assuma que
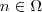
,i.e,
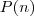
é verdadeiro .
(iii) Mostre que
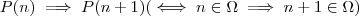
.
Há centenas de exemplos aqui no fórum bem como em outros fóruns e sites .
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
Voltar para Números Complexos
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [hipótese da indução] Indução matemática
por leonardoandra » Sáb Out 12, 2013 22:58
- 1 Respostas
- 2679 Exibições
- Última mensagem por leonardoandra

Seg Out 14, 2013 20:10
Equações
-
- Indução Matemática
por gramata » Qua Set 02, 2009 16:52
- 0 Respostas
- 3062 Exibições
- Última mensagem por gramata

Qua Set 02, 2009 16:52
Problemas do Cotidiano
-
- Indução Matemática
por Abelardo » Qui Mar 31, 2011 03:04
- 1 Respostas
- 2527 Exibições
- Última mensagem por LuizAquino

Qui Mar 31, 2011 11:27
Álgebra Elementar
-
- Indução matemática
por TiagoFERD » Dom Mar 04, 2012 10:08
- 6 Respostas
- 4494 Exibições
- Última mensagem por TiagoFERD

Seg Mar 05, 2012 18:55
Progressões
-
- Indução Matemática
por MateusDantas1 » Dom Mar 04, 2012 13:00
- 1 Respostas
- 1718 Exibições
- Última mensagem por LuizAquino

Ter Mar 06, 2012 01:50
Progressões
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
Unesp - 95 Números Complexos
Autor:
Alucard014 - Dom Ago 01, 2010 18:22
(UNESP - 95) Seja L o Afixo de um Número complexo

em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
Assunto:
Unesp - 95 Números Complexos
Autor:
MarceloFantini - Qui Ago 05, 2010 17:27
Seja

o ângulo entre o eixo horizontal e o afixo

. O triângulo é retângulo com catetos

e

, tal que

. Seja

o ângulo complementar. Então

. Como

, o ângulo que o afixo

formará com a horizontal será

, mas negativo pois tem de ser no quarto quadrante. Se

, então

. Como módulo é um:

.
Logo, o afixo é

.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



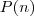 a qual é verdadeira para
a qual é verdadeira para  ,você supõe que para um
,você supõe que para um  arbitrário
arbitrário 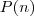 é verdadeira e com base nesta suposição mostra que
é verdadeira e com base nesta suposição mostra que 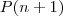 também é verdadeira . Ou seja, você está dizendo que
também é verdadeira . Ou seja, você está dizendo que 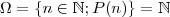 , pois
, pois 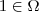 e
e 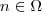 (Hipótese )
(Hipótese ) 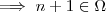 implicando
implicando 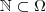 .(Se o todo é sempre maior que qualquer uma de suas partes e esta é maior o todo ; logo só pode ser
.(Se o todo é sempre maior que qualquer uma de suas partes e esta é maior o todo ; logo só pode ser 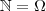 )
)  = o subconjunto dos números naturais
= o subconjunto dos números naturais  para os quais
para os quais 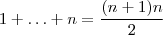 ,i.e,
,i.e, 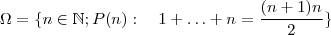 .
.  pertence a
pertence a  ,i.e , checkar se
,i.e , checkar se 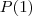 é verdadeiro .
é verdadeiro . 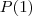 verdadeiro ; assuma que
verdadeiro ; assuma que 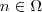 ,i.e,
,i.e, 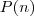 é verdadeiro .
é verdadeiro . 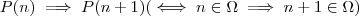 .
. 
 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , mas negativo pois tem de ser no quarto quadrante. Se
, mas negativo pois tem de ser no quarto quadrante. Se  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.