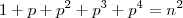Quantos P primos existe para N natural nessas condições?

AjudaMatematica.com! Aqui você compartilha sua dúvida ou solução!

  • Anúncio Global
    Respostas
    Exibições
    Última mensagem

Quantos P primos existe para N natural nessas condições?

Regras do fórum
Responder

Quantos P primos existe para N natural nessas condições?

Mensagempor BrenoNaval » Sex Abr 11, 2014 12:05

1+p+p^2+p^3+p^4=n^2 .Quantos P primos existe para N natural nessas condições?
1 etapa:
Obs.:Vou deixar,algumas de minhas descobertas,espero que possa ajudar.
.(p^5-1)=(p-1)(p^4+p^3+p^2+p+1)
.p^5-1=(p-1)n^2
.n^2= \frac{p^5-1}{p-1}
.\frac{(p-1)!+1}{p}

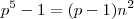
2 etapa:
.p^5-1=0(modp-1)
.p^5=1(modp-1)
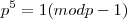
.p^5=p(mod5) =>a^p=a(modp) / p primo,a qualquer.
.p^4=1(mod5) =>a^fi(n)=1(modn) / mdc(a,n)=1.

Obs:a partir da segunda etapa o símbolo = (símbolo de congruência)

.Possíveis algarismos das unidades de n.:{1,5,9},p.:{1,3,7,9}
BrenoNaval
Novo Usuário
Novo Usuário
 
Mensagens: 8
Registrado em: Dom Mar 30, 2014 19:01
Formação Escolar: ENSINO MÉDIO
Andamento: cursando
Voltar ao topo

Re: Quantos P primos existe para N natural nessas condições?

Mensagempor Mattioli » Sex Jun 06, 2014 00:25

1 + p + p^2 + p^3 + p^4 = n^2

Pode-se organizar a equação da seguinte forma:
p(p^1 + p^2 + p^3 + 1) + 1 = n^2

Assim, tem-se uma relação de congruência modulo p, entre 1 e n^2: n^2 \equiv 1(mod p)

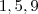Pelo teorema de Euler, dado um número primo p e um número qualquer a, em que os dois são relativamente primos (ou seja, o mdc entre eles é 1), a relação de congruência a^(p-1) \equiv 1(mod p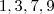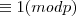) é verdadeira.

Dessa forma, é fácil perceber que o número p que satisfaz essa congruência é o 3, já que a potência do n é 2 e o mesmo é congruente a 1.

Logo, a resposta é: 1 número primo p satisfaz essa equação.
Mattioli
Novo Usuário
Novo Usuário
 
Mensagens: 1
Registrado em: Sex Jun 06, 2014 00:15
Formação Escolar: ENSINO MÉDIO
Área/Curso: A Vida
Andamento: cursando
Voltar ao topo
Responder

Voltar para Aritmética

 


Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!

  • Tópicos relacionados
    Respostas
    Exibições
    Última mensagem

Quem está online

Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes

 


Tópico Popular

Assunto: simplifiquei e achei...está certo?????????????
Autor: zig - Sex Set 23, 2011 13:57

{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}

Assunto: simplifiquei e achei...está certo?????????????
Autor: Vennom - Sex Set 23, 2011 21:41

zig escreveu:{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}


Rpz, o negócio é o seguinte:
Quando você tem uma potência negativa, tu deve inverter a base dela. Por exemplo: {\frac{1}{4}}^{-1} = \frac{4}{1}

Então pense o seguinte: a fração geratriz de 0,05 é \frac{1}{20} , ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
Veja: {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}

A raiz quadrada de vinte, você acha fácil, né?

Espero ter ajudado.

Assunto: simplifiquei e achei...está certo?????????????
Autor: fraol - Dom Dez 11, 2011 20:23

Nós podemos simplificar, um pouco, sqrt(20) da seguinte forma:

sqrt(20) = sqrt(4 . 5) = sqrt( 2^2 . 5 ) = 2 sqrt(5).

É isso.

Assunto: simplifiquei e achei...está certo?????????????
Autor: fraol - Dom Dez 11, 2011 20:24

Nós podemos simplificar, um pouco, \sqrt(20) da seguinte forma:

\sqrt(20) = \sqrt(4 . 5) = \sqrt( 2^2 . 5 ) = 2 \sqrt(5).

É isso.

Powered by phpBB © phpBB Group.

phpBB Mobile / SEO by Artodia.

Índice do fórum